تلخيص وحل أسئلة درس: جمع المتجهات وطرحها – فيزياء 10 «أردني» الفصل الأول

بطاقة الدرس:

• عنوانه: جمع المتجهات وطرحها
• ترتيبه: الثاني من الوحدة الأولى «المتجهات».
• مادة: الفيزياء.
• الصف: العاشر الأساسي.
• الفصل الدراسي: الأول.
• المدارس: الأردنية.
• الهدف: شرح وتلخيص/مراجعة وحل أسئلة.
• الدرس السابق: الكميات القياسية والكميات المتجهة

جمع المتجهات

تعلمنا سابقا أنه بمكن ضرب الكميات المتجهة والكميات القياسية، سنتعلم في هذا الفصل كيف يمكننا جمع وطرح الكميات المتجهة وما هو الفرق بين جمع وطرح الكميات المتجهة والكميات القياسية؟

• الكميات القياسية يتم جمع وطرحها بطريقة جبرية بشرط أن تكون من النوع نفسه ولها الوحدات نفسها ويكون ناتج الجمع كمية قياسية أيضا.

كمثال على جمع وطرح الكميات القياسية:

كتلة معاذ (50 كغم) وكتلة احمد (40 كغم) فما هو مجموع كتلة كل منهما؟

الحل:

مجموع كتلة معاذ واحمد = 50+ 40 = 90 كغم. ← (جمع وطرح جبري رياضي)

• الكميات المتجهة يجب مراعاة الاتجاه والمقدار عند جمعها أو طرحها.

كمثال على جمع وطرح الكميات المتجهة:

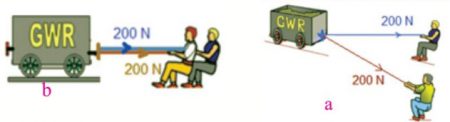
في الشكل (a) لو قمنا بجمع القوتان اللتان يؤثر بهما الرجلان لسحب العربة بشكل جبري (400N = 200N + 200N) فإن الإجابة تكون غير صحيحة.

أما إذا أثر الرجلان في الاتجاه نفسه كما في الشكل (b) فأنه لو قمنا بجمع القوتان اللتان يؤثر بهما الرجلان لسحب العربة بشكل جبري (400N= 200N + 200N) فإن الإجابة تكون صحيحة.

• ناتج جمع متجهين مثل (A) و (B) يكون متجه جديد (A+B) يختلف مقداره واتجاهه باختلاف مقدار واتجاه كل من المتجهين، وما ينطبق على جمع متجهين ينطبق على جمع عدة متجهات.
• يسمى المتجه الناتج من جمع عدة متجهات باسم (متجه المحصلة) ويرمز له بالرمز (R).

R=A+B+C

بشرط أن تكون المتجهات من النوع نفسه كمثال إذا جمعنا متجهات سرعة يكون متجه المحصلة متجه سرعة وهكذا…

سؤال: وضح ما هو المقصود بمتجه المحصلة؟

ج: المتجه الناتج عن الجمع المتجهي لعدة متجهات.

سؤال: مزلاج كتلته (m1=70 kg) وضع فوقه صندوق حجمه (1m³) وكتلته (m2=80kg)، سحب المزلاج بقوة مقدارها (F1=400N) باتجاه الشرق وأثرت في المزلاج قوة أخرى (100N =F2) باتجاه الغرب فتحرك المزلاج بتسارع (a=2 m/s²) باتجاه الشرق؟

1) حدد الكميات القياسية التي يمكن جمعها معًا وجد ناتج جمعها؟

الحل:

الكميات القياسية في المثال هي كتلة المزلاج وحجم الصندوق وكتلة الصندوق.

الكميات التي يمكن جمعها يجب أن تكون من النوع نفسه وهي (70kg=m1) و (m2=80 kg) وناتج جمعها هو كمية قياسية (m1+m2) وتساوي (150 = 80+70).

2) حدد الكميات المتجهة التي يمكن جمعها معًا وعبر عن ناتج جمعها (المحصلة) بالرموز؟

الحل:

الكميات المتجهة هي القوة الأولى (F1) والقوة الثانية (F2)، التسارع (a).

الكميات التي يمكن جمعها يجب أن تكون من النوع نفسه وهي (400N=F1) و (F2=100N) ومحصلتها:

(R=F1 + F2) وهي كمية متجهة.

طرح المتجهات

• مشابهة لعملية الجمع والإشارة السالبة تدل على معكوس المتجه المراد طرحه.

كمثال عند طرح المتجه (A) من المتجه (B) أي ( A – B):

فإن المتجه (A) يجمع مع معكوس المتجه الثاني (B-) ويكتب بالصورة:

(A – B = A+(-B

سؤال: وضح ما هو المقصود بطرح المتجه؟

ج: جمع سالب ذلك المتجه.

محصلة متجهات عدة

لإيجاد محصلة متجهين أو أكثر بغض النظر عن كونه في بعد واحد مثل محور (x) أو (y) أو في بعدين مثل مستوى (x-y) فإننا نستخدم إحدى الطريقتين:

1. الطريقة البيانية (الرسم).
2. الطريقة التحليلية.

الطريقة البيانية (الرسم):

تمثيل المتجهات المراد جمعها بأسهم ثم تركيب هذه الأسهم من خلال طريقتين إما بطريقة متوازي الأضلاع أو بطريقة المضلع (الذيل على الرأس).

والطريقة المتناولة والمطلوبة منا في الكتاب الحالي هي طريقة المضلع فقط.

طريقة المضلع (الذيل إلى الرأس):

• اختيار مقياس مناسب ورسم أسهم تمثل كل متجه لإيجاد محصلتها.
• رسم المتجه الأول ثم نرسم المتجه الثاني بحيث نضع ذيل المتجه الثاني عند رأس المتجه الأول وعلى هذا الحال لباقي المتجهات حتى نصل لآخر متجه.
• يجب المحافظة على طول واتجاه السهم عند نقله ووضعه.
• في النهاية نرسم سهم يصل بين ذيل المتجه الأول ورأس المتجه الأخير ويكون طوله عبارة عن مقدار محصلة المتجهات جميعها واتجاه من الذيل على الرأس يدل على اتجاه متجه المحصلة.
• دائما نأخذ ونقيس الزاوية بين متجه المحصلة ومحور السينات الموجب (x+) ونقوم بقياسها باستخدام المنقلة.

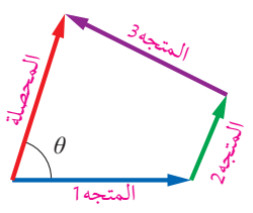
سؤال: هل يمكن إيجاد الزاوية (θ) بطريقة رياضية من دون استخدام المنقلة؟

الإجابة:

نعم يمكن ذلك في حالات خاصة كمثال إذا تم جمع متجهين وإيحاد محصلة المتجهين وأعطانا شكل مثلث قائم فيمكننا باستخدام قوانين المثلث القائم إيجاد الزاوية.

المتجه = الذيل ← الرأس

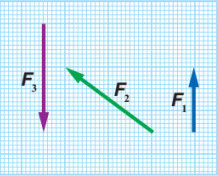
سؤال: تؤثر ثلاث قوى في جسم: القوة الأولى (F1) مقدارها (30N) في اتجاه الشمال، والقوة الثانية (F2) مقدارها (50N) في اتجاه يصنع زاوية مقدارها (°37) شمال الغرب، والقوة الثالثة (F3) مقدارها (60N) في اتجاه الجنوب.

جد مقدار واتجاه محصلة القوى المؤثرة في الجسم بيانيًا؟

الحل:

بالبداية قبل أي شيء من خلال الاطلاع على مقدار كل متجه نحدد مقياس رسم مناسب للرسم وليكن (cm1: N10) وبالتالي يكون طول كل متجه من المتجهات كالآتي:

• F1→3cm
• F2→5cm
• F3→6cm

الآن نرسم كل متجه لوحدة على الرسم البياني ضمن مقياس الرسم المتفق عليه أعلاه…

F1 باتجاه الشمال بطول (3cm) ←

F3 باتجاه الجنوب بطول (6cm) ←

F2 بما ان اتجاه المتجه يصنع زاوية (°37) مع شمال الغرب فذلك يعني أن الزاوية مصنوعة بين المتجه والمحور الذي فيه ال التعريف وهو الغرب في حالتنا هذه، فنرسم سهما طوله (5cm) يصنع زاوية (°37) مع محور ال غرب (x-).

الآن نرسم السهم الذي يمثل (F1) ثم نرسم السهم الذي يمثل (F2) بحيث ذيله على رأس سهم (F1)، ثم نرسم السهم الذي يمثل (F3) بحيث ذيله على رأس سهم (F2).

بعد ذلك نرسم سهما من ذيل المتجه الأول (F1) إلى رأس المتجه الثالث الأخير (F3) ليمثل طوله مقدار المحصلة ويمثل اتجاهه اتجاه المحصلة.

 

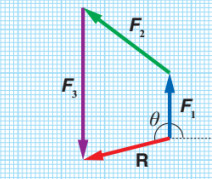
نقيس بالمسطرة طول سهم المحصلة (R) في الشكل وحسب مقدار مقياس الرسم.

نستطيع معرفة مقدار المحصلة، وفي شكلنا ومثالنا من الكتاب تبين معنا بإن طول السهم (4.1cm) وبحسب مقياس الرسم (cm1: N10) فإن مقدار المحصلة يساوي (41N).

ونقيس بالمنقلة الزاوية بين متجه المحصلة (R) و محور (x+) ← 194° لتمثل اتجاه المحصلة.

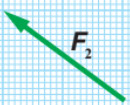
سؤال: شحنة كهربائية تؤثر فيها ثلاث قوى كهربائية على النحو الآتي (F1) مقدارها (200N) في اتجاه الجنوب، والقوة الثانية (F2) مقدارها (300N) في اتجاه يصنع زاوية مقدارها (°53) شمال الغرب، والقوة الثالثة (F3) مقدارها (500N) في اتجاه الغرب. جد مقدار محصلة القوى المؤثرة في الشحنة واتجاهها بيانيًا?

الإجابة:

نفس آلية الحل السابقة من خلال الاطلاع على مقدار كل متجه نحدد مقياس رسم مناسب للرسم وليكن (cm1: N10) وبالتالي يكون طول كل متجه من المتجهات كالآتي:

• 2cm ←F1

• 3cm ←F2

• 5cm  ←F3

الآن نرسم كل متجه لوحدة على الرسم البياني ضمن مقياس الرسم المتفق عليه أعلاه…

• F1 باتجاه الجنوب بطول (2cm).
• F3 باتجاه الغرب بطول (5cm).
• F2 بما ان اتجاه المتجه يصنع زاوية (°53) مع شمال الغرب فذلك يعني أن الزاوية مصنوعة بين المتجه والمحور الذي فيه ال التعريف وهو الغرب في حالتنا هذه، فنرسم سهما طوله (3cm) يصنع زاوية (°53) مع محور ال غرب (x-).

الآن نرسم السهم الذي يمثل (F1) ثم نرسم السهم الذي يمثل (F2) بحيث ذيله على رأس سهم (F1)، ثم نرسم السهم الذي يمثل (3)F) بحيث ذيله على رأس سهم (F2).

بعد ذلك نرسم سهما من ذيل المتجه الأول (F1) إلى رأس المتجه الثالث الأخير (F3) ليمثل طوله مقدار المحصلة ويمثل اتجاهه اتجاه المحصلة.

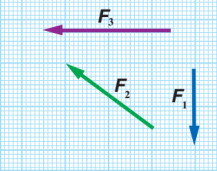
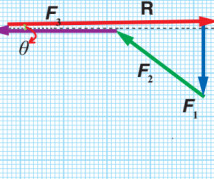
نقيس بالمسطرة طول سهم المحصلة (R) في الشكل وحسب مقـ مقياس الرسم نستطيع معرفة مقدار المحصلة، ونقيس بالمنقلة الزاوية بين متجه المحصلة (R) ومحور (x-) لتمثل اتجاه المحصلة.

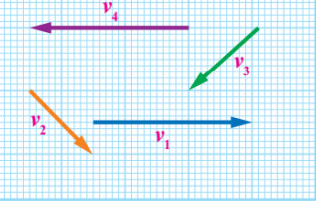
سؤال: مثلث أربعة متجهات للسرعة (v1, v2,v3,v4) بالرسم كما في الشكل وذلك باستخدام مقياس رسم (1cm: 5m/s) (1)، جد ما يلي:

1) مقدار متجه محصلة السرعة واتجاهه؟

الحل:

من خلال تطبيق طريقة المضلع يكون طول سهم المحصلة (4cm) وحسب مقياس الرسم (1cm: 5m/s) فإن مقدار المتجه المحصل (20m/s) واتجاهها من خلال المنقلة يكون نحو الجنوب بزاوية (°270).

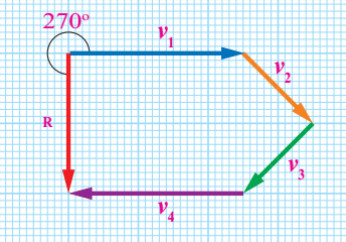
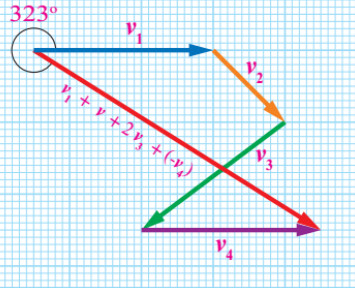
2) مقدار متجه واتجاه محصلة (V1 + V2 + 2V3 -V4)؟

الحل:

بتطبيق طريقة المضلع يكون طول سهم المتجه الناتج من جمع (V1 + V2 + 2V3 -V4) هو (10cm) وحسب مقياس الرسم (1cm: 5m/s) فإن مقدار المتجه المحصل (ms (50m/s واتجاهها باستخدام المنقلة يميل بزاوية (°323) عن محور (x+).

سؤال: ما هي عيوب وسلبيات استخدام الطريقة البيانية (الرسم) لإيجاد محصلة المتجهات؟

ج: نتائجها تكون غير دقيقة بسبب أخطاء في عمليات القياس عند قياس الأطوال والزوايا.

الطريقة التحليلية

طريقة أكثر دقة لإيجاد محصلة المتجهات من خلال تحليل المتجهات إلى مركباتها بحيث نقوم بتحليل المتجه الواحد والاستعاضة عنه بمتجهين متعامدين (على محوري (y) و(x) مثلا) يسميان مركبتي المتجه وتكون محصلتهما المتجه نفسه ويتحدان معه في نقطة البداية.

عملية تحليل المتجه

يمكن تحليل المتجه إلى مركبتين مركبة أفقية ومركبة عمودية كمثال سنقوم بتحليل المتجه (A) الواقع في الربع الأول من مستوى (x-y) كما في الشكل 

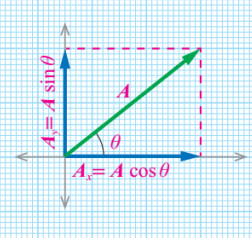
إلى مركبتين هما:

• المركبة الأفقية (Ax): تمثل مسقط المتجه (A) على محور (x+).
• المركبة العمودية (Ay): تمثل مسقط المتجه (A) على محور (y+).

ملاحظات مهمة:

• يكون المجموع المتجهي للمركبتين مساويا للمتجه (A):

Ay + Ax = A

• يمكننا تطبيق النسب المثلثية لإيجاد قيمة كل من المركبة الأفقية والعمودية:

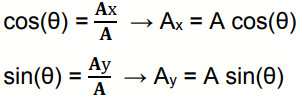
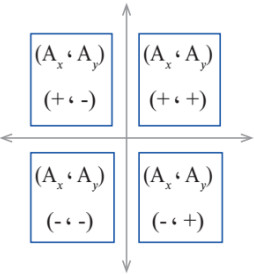
• تتغير إشارة المركبات الأفقية والعمودية بحسب الربع الذي يقع فيه المتجه.

لاحظ معنا الشكل: المركبتان (Ax) و (Ay) تشكلان ضلعين في مثلث قائم الزاوية والمتجه (A) يمثل وتر هذا المثلث القائم لذلك يمكننا استخدام قانون فيثاغورس في هذه الحالة:

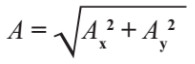
ويمكننا حساب الزاوية المرجعية بين المتجه ومحور () من خلال العلاقة الآتية:

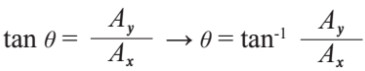
إذا حصلنا على أكثر من قيمة للزاوية فإنه يمكننا تحديد القيمة الصحيحة بينهما من خلال إشارة كل من المركبتين (Ax) و (Ay) فإن كانت الإشارتين موجبتين دل ذلك على أن المتجه يقع في الربع الأول فنختار الزاوية التي تقع في الربع الأول وهكذا..

سؤال: ما المقصود بتحليل المتجه؟

ج: استبدال متجه بمتجهين متعامدين يسميان مركبتي المتجه ومحصلتهما المتجه نفسه ويتحدان معه في نقطة البداية.

سؤال: تتحرك مركبة بتسارع ثابت (°150 , a=6m/s²) جد مقدار المركبتين الأفقية والعمودية للتسارع وحدد اتجاههما؟

الحل:

نبحث عن زاوية مرجعية لتسهيل آلية الحل معنا ونحن في هذا المثال اخترنا الزاوية (°30) وهي متممة زاوية (°150).

عند تحليل المتجه لمركبتين دائما تكون (cos) مع المحور الذي نختار معه الزاوية.

ax =a cos (30°) = 6 ×-cos (30°)

ay =a sin (30°) = 6 sin (30°)

مهم جدًا: الجيب يكون موجب في الربع الثاني والجتا يكون سالب لذلك وضعنا معه إشارة سالبة

ax =a cos (30°) = 6 ×-cos (30°) = -5.2 m/s²

ay =a sin(30°) = 6 × sin(30°) = +3 m/s²

لاحظ معي أن إشارة (ax) سالبة مما يعني أن اتجاهها نحو محور (x-) وإشارة (ay) موجبة مما يعني أن اتجاهها نحو محور (y+) وبالتالي المتجه (a) يقع في الربع الثاني.

سؤال: يسحب عامر صندوق ألعابه بقوة مقدارها (100N) في اتجاه يصنع زاوية مقدارها (°30) مع محور (x+)، جد مقدار كل من المركبتين الأفقية والعمودية للقوة محددًا اتجاه كل منهما؟

الحل:

الآن بما أن الزاوية جاهزة أمورها تمام التمام نبدأ فورًا بالمركبات الأفقية والعمودية.

عند تحليل المتجه لمركبتي ن دائما تكون (cos) مع المحور الذي نختار معه الزاوية.

Fx =F cos (30°) = 100 cos (30°)

Fy =F sin(30°) = 100 sin(30)

مهم جدًا: الجيب والجتا يكون موجب في الربع الأول.

Fx =F cos (30°) = 100 cos (30°) = 100 × 0.87 = 87 N

Fy =F sin (30°) = 100 sin(30°) = 100 × 0.5 = 50 N

سؤال: أطلقت قذيفة بسرعة (٧) وكانت المركبة الأفقية للسرعة  (20m/s-) والمركبة العمودية لها  (40m/s)، جد مقدار السرعة (٧) واتجاهها ومثل ذلك بيانيًا؟

الحل:

vx= -20 m/s , Vy = 40 m/s

 ؟!= θ

؟!= v

يمكننا حساب مقدار متجه السرعة من خلال:

لاحظ أن إشارة (Vx) سالبة مما يعني أن اتجاهها نحو محور ( x- ) وإشارة (ay) موجبة مما يعني أن اتجاهها نحو محور (y+) وبالتالي المتجه (a) يقع في الربع الثاني.

أي أن الزاوية الصحيحة هي (°117 =θ).

سؤال: تؤثر القوتان (F1) و (F2) في نقطة مادية كما في الشكل، جد مقدار كل من المركبتين الأفقية والعمودية لكل قوة محددًا اتجاه كل منهما؟

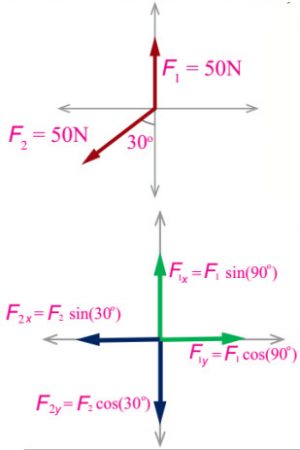
الحل:

بالبداية نقوم بإيجاد المركبة العمودية والأفقية للمتجه الأول:

F1x=F1 cos (90°) = 50 × 0 = 0

F1y= F1 sin (90°) = 50 × 1 = 50 N

ثم نقوم بإيجاد المركبة العمودية والأفقية للمتجه الأول:

F2x=F2 cos (30°) = 50 × 0.86 = 43

F2y = F2 sin(30) = 50 × 0.5 = 25 N

محصلة المتجهات بالطريقة التحليلية

لإيجاد مقدار واتجاه محصلة متجهين أو أكثر بالطريقة التحليلية نتبع الخطوات الآتية:

• نرسم المتجهات بحيث يبدأ كل متجه من نقطة الأصل (0,0) عند رسمه.
• نحلل كل متجه إل مركبتي العمودية والأفقية مع مراعاة التقاء نقطة البداية لكل متجه عند نقطة الأصل.
• نجد محصلة المركبات على محور (X) من خلال جمع متجهات المركبة الأفقية ← Rx.

نجد محصلة المركبات على محور (y) من خلال جمع متجهات المركبة العمودية ←Ry.

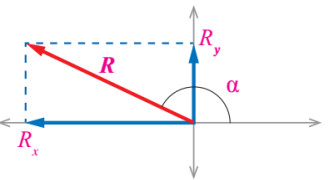
• نجد مقدار المحصلة الكلية للمتجهات (R) باستخدام العلاقة ←
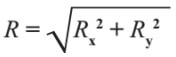
• نحدد اتجاه المحصلة الكلية للمتجهات (R) باستخدام العلاقة ←

حيث (a) هي الزاوية بين (R) ومحور (x+).

• المركبة التي يكون مقدارها (0) بسبب الزاوية لا داعي لوضعها في الرسم عند تحليل المركبات.

1. Rx موجب ← نحو محور (x+).
2. Rx سالب ← نحو محور (x-).
3. Ry موجب ← نحو محور (y+).
4. Ry سالب ← نحو محور (y-).

سؤال: ثلاثة متجهات (A) و (B) و (C) قيمها: 2u ,5u , 3u على الترتيب كما في الشكل جد مقدار المحصلة واتجاهها بالطريقة التحليلية؟

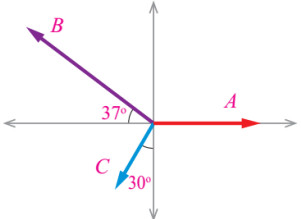
الحل:

نحلل كل متجه إلى مركبته العمودية والأفقية:

Ax= Acos (0°) = 3 × 1 = 3 u

Ay = A sin (0°) = 3×0 = 0

Bx = B cos (37°) = 5 x -0.8= -4 u

By = B sin (37°) = 5 × 0.6 = 3 u

Cx = C cos (240°) =C sin (30°) = 2 × -0.5 = -1 u

Cy = C sin (240°) = C cos (30°) = 2 × -0.87 = -1.74 u

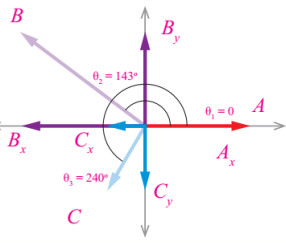
الآن نجد محصلة المتجهات على محور (X):

Rx = Ax + Bx + Cx = 3 + 4 + −1 = -2 u

الآن نجد محصلة المتجهات على محور (y):

Ry = Ay + By + Cy = 0 + 3 + -1.74 = 1.26 u

الآن نجد مقدار محصلة المتجهات الكلية (R):

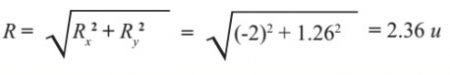
نجد مقدار الزاوية بين (R) ومحور (x+):

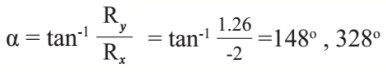
تهمل الزاوية (°328) ونختار الزاوية (°148) لأنه من خلال الشكل والرسم يتبين بأن الزاوية تقع في الربع الثاني.

سؤال: ثلاثة متجهات (A) و (B) و (C) قيمها: 2u ,5u , 3u على الترتيب كما في الشكل جد مقدار المحصلة واتجاهها بيانيا (بالطريقة البيانية)؟

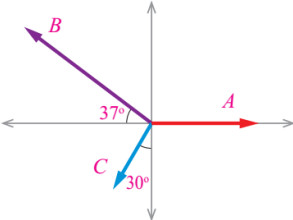
الحل:

نفس آلية الحل السابقة من خلال الاطلاع على مقدار كل متجد للرسم وليكن (1cm:1u) وبالتالي يكون طول كل متجه من:

• A←3cm
• B←5cm
• C←2cm

الآن نرسم كل متجه لوحدة على الرسم البياني ضمن مقياس الرسم المتفق عليه أعلاه.

الآن نرسم السهم الذي يمثل (A) ثم نرسم السهم الذي يمثل (B) بحيث ذيله على رأس سهم (A)، ثم نرسم السهم الذي يمثل (C) بحيث ذيله على رأس سهم (B).

بعد ذلك ترسم سهما من ذيل المتجه الأول (A) إلى رأس المتجه الثالث الأخير (C) ليمثل طوله مقدار المحصلة ويمثل اتجاهه اتجاه المحصلة.

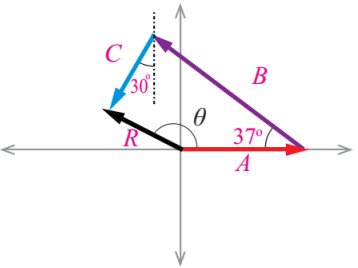
نقيس بالمسطرة طول سهم المحصلة (R) في الشكل وحسب مقدار مقياس الرسم نستطيع معرفة مقدار المحصلة، بعد القياس تبين أن طوله (2.36cm).

ومن خلال مقياس الرسم مقدار المتجه = (2.36u) ونقيس بالمنقلة الزاوية بين متجه المحصلة (R) ومحور (x+) لتمثل اتجاه المحصلة، وبعد القياس تبين أن مقدار الزاوية (θ) هو (°148).

مراجعة بسيطة

إذا لم يصرح السؤال باستخدام الطريقة البيانية أو التحليلية لإيجاد المحصلة يمكننا استخدام قوانين المتجهات كما أخدنا سابقا في الدورة التأسيسية:

• إذا كانت القوتان في الاتجاه نفسه فان محصلتهما:

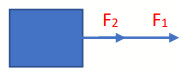
اتجاهاً: (في نفس اتجاه القوتين).

مقداراً: (R = F1 + F2).

• إذا كانت القوتان في اتجاهين متعاكسين فان محصلتهما:

اتجاهاً: (في اتجاه الكبرى منهما).

مقداراً: R = F min – F max.

• إذا كانت القوتان متعامدتين بينهما زاوية (90) فان محصلتهما:

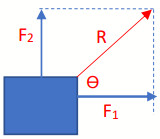مقداراً:

اتجاهاً:

• إذا كانت القوة غير منطبقة على المحاور الرئيسية نقوم بـ (التحليل إلى مركبات) مركبتين (سينية وصادية ويتم توزيع الـ جا θ وجتا θ حسب مكان صنع الزاوية θ.
• إذا كانت المحصلة الكلية للقوة تساوي صفر فذلك يعني أن محصلة القوى الأفقية تساوي صفر ومحصلة القوى العمودية تساوي صفر.

سؤال: تؤثر ثلاثة قوى في نقطة مادية كما في الشكل، فإذا علمت أن محصلة تلك القوى تساوي صفرًا، فجد مقدار كل من القوتين الأولى والثانية؟

الحل:

بما أن السؤال لم يلزمنا باتباع الطريقة التحليلية أو البيانية نقوم بالحل باستخدام قوانين المتجهات كما أخدنا في دورة التأسيس محصلة القوة = صفر ذلك يعني أن:

محصلة القوة العمودية = صفر، محصلة القوة الأفقية = صفر.

نقوم بتحليل أي متجه ليس على المحاور الرئيسية إلى مركبتين أفقية وعمودية ثم نتبع قواعد جمع وطرح المتجهات.

F2 = F3x→ F2 = 50 sin(60) = 25√3 N

F1 = F3y → F1 = 50 cos(60) = 25 N

حل أسئلة مراجعة الدرس الثاني من الوحدة الأولى

سؤال 1: قارن بين كل مما يأتي:

• جمع المتجهات وتحليلها:

ج: جمع المتجهات جمع متجهي للكميات المتجهة يراعي فيه المقدار والاتجاه وليس جمع جبري أما تحليل المتجهات يتم من خلال استبدال متجه بمتجهين متعامدين يسميان بمركبتي المتجه ومحصلتهما المتجه نفسه.

• جمع المتجهات ومحصلتها:

ج: جمع المتجهات جمع متجهي للكميات المتجهة يراعي فيه المقدار والاتجاه وليس جمع جبري أما محصلة المتجهات هو متجه ناتج عن الجمع المتجهي لعدة متجهات.

• جمع المتجهات وطرحها:

ج: جمع المتجهات جمع متجهي للكميات المتجهة يراعي فيه المقدار والاتجاه وليس جمع جبري أما طرح المتجهات هو جمع سالب الكميات المتجهة.

• الطريقة التحليلية والطريقة البيانية في جمع المتجهات:

ج: في الطريقة البيانية نقوم بتمثيل المتجهات المراد جمعها بأسهم ثم تركيب هذه الأسهم.

أما في الطريقة التحليلية نقوم بالجمع الرياضي لإيجاد محصلة متجهين أو اكثر من خلال تحليل كل متجه إلى مركباته.

سؤال 2: اكمل الفراغ بما هو مناسب في الجدول الآتي الذي يمثل تحليل المتجهات إلى مركباتها:

المتجه	المركبة الأفقية	المركبة العمودية
°d=8m , 53	8xcos(53°)	8xsin(53°)
	6N	-8 N
	10m/s

سؤال 3: اعتمادًا على الشكل المجاور:

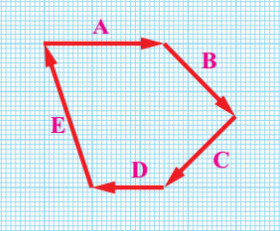
• ما محصلة المتجهات المبينة في الرسم؟

ج: A+B+C+D+E

• جد بيانيًا محصلة المتجهين: A و B:

الحل:

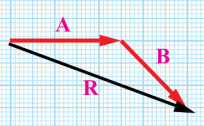
أثبت بالرسم أن: (A+B+C=-D+(-E:

الحل:

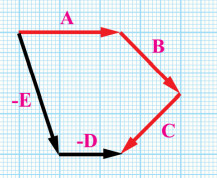
سؤال 4: قوتان متساويتان في المقدار، ما أكبر قيمة لمحصلتهما؟ وما أقل قيمة لمحصلتهما؟

الإجابة:

أكبر قيمة لمحصلتهما عندما تكون القوتان في نفس الاتجاه أي ان الزاوية بينهما (0). وأقل قيمة لمحصلتهما عندما تكون القوتان متعاكسان في الاتجاه أي ان الزاوية بينهما (180).

سؤال 5: ما مقدار الزاوية التي تطلق بها كرة القدم بسرعة متجهة (V) بحيث:

 تساوي المركبة العامودية للسرعة (Vy) صفرًا:

ج: المركبة العامودية ← (θ)Vy = V×sin) وتكون المركبة العامودية صفر عندما تكون الزاوية (0) أو (180).

تساوي المركبة الأفقية للسرعة ( Vx ) متجه السرعة (V):

ج: المركبة العامودية ← (θ)Vy = V×cos وتكون (۷) مساوية لـ (Vx) عندما تكون الزاوية (0).

سؤال 6: ثلاث جرارات تحاول سحب صخرة كبيرة. إذا أثر كل منها بقوة سحب مقدارها (N 4000 في الاتجاهات المبينة في الشكل:

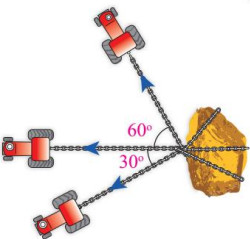
1. جد مقدار محصلة القوى التي تؤثر بها الجرارات في الصخرة؟

الحل:

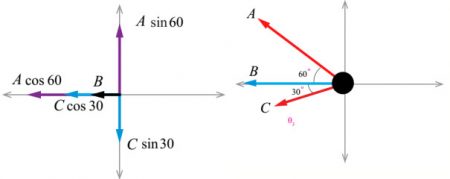
Rx = A cos(60) + B + C cos(60) = 4000 × 0.5 + 4000 + 4000 × 0.5 = 6000 N

Ry = A sin(60) – C sin(30) = 4000 × 0.87 – 4000 × 0.5 = 1480 N

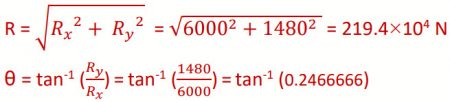
2. في أي اتجاه ستتحرك الصخرة؟

ج: في الاتجاه شمال الغرب بحيث تصنع زاوية مقدارها (0.2466666) tan⁻¹ مع محور (x-).