بطاقة المحتوى:
- عنوان الوحدة: المتجهات.
- دروسها/فصولها: 1. الكميات القياسية والكميات المتجهة 2. جمع المتجهات وطرحها
- مادة: الفيزياء.
- الصف: العاشر الأساسي.
- الفصل الدراسي: الأول.
- المدارس: الأردنية.
- الهدف: حل الأسئلة.
سؤال 1: ضع دائرة حول رمز الإجابة الصحيحة لكل مما يأتي:
- الكمية المتجهة من الكميات الفيزيائية الآتية هي:
تسارع الطائرة في أثناء إقلاعها (c)
عند جمع القوتين (30N) و (20N) جمعًا متجها، فإن الناتج غير الصحيح من النواتج المحتملة الآتية هو:
55N والسبب في ذلك إنه مستحيل الحصول على هذه القيمة سواء كان المتجهان على نفس الخط متعاكسان أو في نفس الجهة أو متعامدان دائما تكون المحصلة أقل من مجموعها.
- حاصل الضرب المتجهي | AXB | في الشكل المجاور هو:
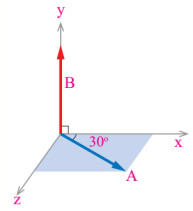ABsin90°
- العلاقة بين متجهي التسارع a1 , a2 بناء على العلاقة ( 0 = a1-a2 ) هي:
المتجهان a1,a2 متساويان في المقدار ومتعاكسان في الاتجاه.
- المقدار والاتجاه لمحصلة القوى في الشكل المجاور هما:
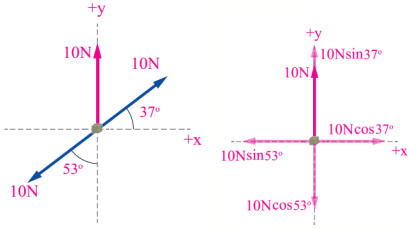
10N, +y
لاحظ أن:
cos53°=sin37°. sin53°=cos37°
- صوبت سعاد كرة السلة بسرعة مقدارها (20m/s) في الاتجاه المبين في الشكل. أي الآتية تمثل المركبة الأفقية للسرعة:
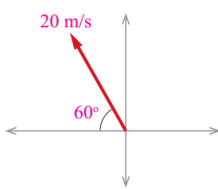
20cos 120°
سؤال 2: ركل لاعب كرة قدم كتلتها )0.4Kg) لتنطلق بسرعة (30m/s) في اتجاه يصنع زاوية °37 مع سطح الأرض الأفقي وبتسارع مقداره (²10m/s). وقد استغرقت الكرة مدة زمنية مقدارها 6s لتعود إلى مستوى سطح الأرض.
حدد الكميات المتجهة والكميات القياسية؟
الإجابة:
الكميات المتجهة ← (السرعة) و (التسارع).
الكميات القياسية ← (كتلة الكرة) و (المدة الزمنية للعودة لسطح الأرض) و (الزاوية).
مثل الكميات المتجهة بيانيًا؟
الحل:
نختار مقياس رسم مناسب لكل متجه ولنفرض هنا أخترنا (²1cm=10m/s)،(1cm 10m/s).
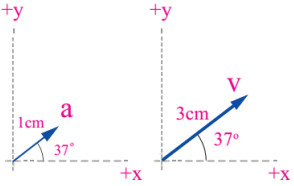
هل يمكن إيجاد محصلة تلك الكميات المتجه؟
ج: نعم يمكن من خلال تحليل المتجه لمركبتين عمودية وأفقية.
سؤال 3: تؤثر قوى عدة في جسم كما في الشكل المجاور.. جد المقدار والاتجاه لمحصلة القوى المؤثرة في الجسم بالطريقة التحليلية؟
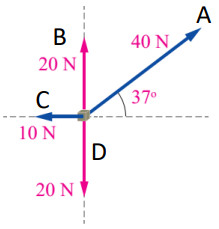
الحل:
نحلل كل متجه إلى مركبته العمودية والأفقية.
Ax = A cos(37°) = 40 x 0.76 = 30.61 u
Ay = A sin(37°) = 40 × 0 = 0
Bx=B cos(90°) = 20 × 0 = 0
By = B sin(90°) = 20 × 1 = 20 u
Cx = C cos(180°) = 10x-1=-10 u
Cy = C sin(180°) = 10 × 0 = 0
Dx = D cos(270°) = 20 × 0 = 0
Dy =D sin(270°) = 20x-1=-20 u
الآن نجد محصلة المتجهات على محور (X):
Rx = Ax + Bx + Cx + Dx = 30.61 + 0 + -10 + 0 = 20.61 u
الآن نجد محصلة المتجهات على محور (۷):
Ry = Ay + By + Cy+ Dy = 0 + 20 + 0 + 20 = 0
الآن نجد مقدار محصلة المتجهات الكلية (R):
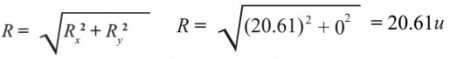
نجد مقدار الزاوية بين (R) ومحور (x+):
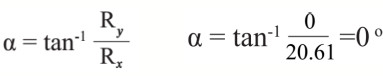
سؤال 4: متجهان الأول F=8N في اتجاه محور (y-) والثاني r=5m في اتجاه محور (+x) جد:
- 3XF = 3×8 = 24N ← 3F.
- 0.5xr = -0.5×5 = -2.5m ← -0.5r-
- rxF = rFsin90° = 5×8×1 = 30N ← rxF
- rxr = rr sin0° = 5×5×0 = 0 ← rxr
- r.F = Frcos90° = 8×5×0 = 0 ← F.r
سؤال 5: انطلقت نور من منزلها سيرًا على الأقدام وقطعت مسافة (400m) باتجاه الغرب، ثم اتجهت شرقًا وقطعت مسافة (200m) لتصل منزل صديقتها. إذا أرادت نور العودة مباشرة إلى منزلها بخط مستقيم، فكم مترًا يجب أن تسير؟ وفي أي اتجاه يتعين عليها السير حتى تصل منزلها؟
ج: 200m نحو الغرب حتى تصل منزلها.
سؤال 6: ثلاثة متجهات للسرعة تشكل مثلثا مغلقا كما في الشكل المجاور. جد:
الإجابة:
- V1+V2= V1+V2 =V3 = 45 m/s
- محصلة المتجهات الثلاثة: 0 = V1 + V2 + V3.
سؤال 7: صوبت سارة كرة تنس أفقيا نحو حائط عمودي فاصطدمت به بسرعة أفقية V1 مقدارها m/s 10 باتجاه الشرقK ثم ارتدت عنه أفقيا نحو الغرب بسرعة V2 مقدارها m/s 7. جد التغير في سرعة الكرة (Δ۷).
الحل:
ΔV = V2 – V1 = 7 m/s – 10 m/s = -3 m/s
نحو الغرب (الإشارة سالبة).
سؤال 8: ما مقدار الزاوية بين المتجهين (A) و (B) في الحالتين الآتيتين:
θ = 90° → sin θ = 1 → ABsine= AB
θ = 0° → cos θ = 1 → ABcose = AB →A.B=AB
سؤال 9: أستخدم الطريقة البيانية في حساب ناتج جمع المتجهات وطرحها كما هو مبين في الجدول الآتي:
الإجابة:
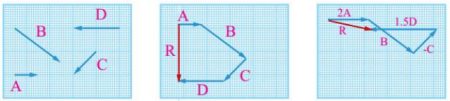
المحصلة R
المُتَّجِهاتُ: D، C، B،A
حيث يُمثْلُ كُلُّ مربع في الرسم وحدةً واحدةً (1u).
ناتج جمع: B – C + 1.5 D +2A.
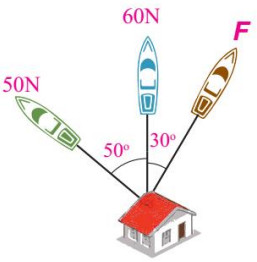
سؤال 10: ثلاثة قوارب كل منها يؤثر بقوة في منزل عائم في الماء لسحبه كما في الشكل المجاور. فإذا تحرك المنزل باتجاه محور (y+) جد:
- مقدار القوة (F):
- مقدار محصلة القوى الثلاث واتجاهها:
