تلخيص وحل أسئلة درس: الكميات القياسية والكميات المتجهة – فيزياء 10 «أردني» الفصل الأول

بطاقة الدرس:

• عنوانه: الكميات القياسية والكميات المتجهة
• ترتيبه: الأول من الوحدة الأولى «المتجهات».
• مادة: الفيزياء.
• الصف: العاشر الأساسي.
• الفصل الدراسي: الأول.
• المدارس: الأردنية.
• الهدف: شرح وتلخيص/مراجعة وحل أسئلة.

الكميات الفيزيائية

نتعامل في حياتنا اليومية مع كميات فيزيائية عديدة يتم التعبير عنها بعدد ووحدة مناسبتين فمثلا نقول (كتلة الحقيبة = (2كغ) حيث (2) تمثل العدد و (كغ) تمثل الوحدة.

يمكن تقسيم الكميات الفيزيائية إلى:

• كميات أساسية: هي الكمية التي تعرف بمقدار واحد فقط دون الحاجة إلى كمية فيزيائية أخرى لتعريفها. وهي سبعة كميات متفق عليها في النظام الدولي: (الزمن ودرجة الحرارة والكتلة والطول والشحنة والتيار الكهربائي وشدة الضوء وكمية المادة).
• كميات مشتقة: وهى الكمية التي يتم استنتاجها من الكميات الأساسية أي أننا نحتاج في تعريفها الى أكثر من كمية أساسية مثل السرعة والتي تساوى مقسوم المسافة على الزمن. من الأمثلة عليها: القوة والسرعة والتسارع.

بشكل عام تقسم الكميات الفيزيائية إلى قسمين رئيسين هما:

• الكميات القياسية: هي الكميات التي تحدد فقط بالمقدار ولا يوجد لها اتجاه. من الأمثلة عليها: الحجم، الطاقة، الضغط، المسافة.
• الكميات المتجهة: هي الكميات التي تُحدد بالمقدار والاتجاه معا. من الأمثلة عليها: الإزاحة، التسارع، القوة.

سؤال: صنّف الكميات الفيزيائية الآتية إلى كميات متجهة أو قياسية؟

الكمية الفيزيائية	كمية متجهة / كمية قياسية	السبب
الكتلة (4Kg)	قياسية	لأنها حددت فقط بمقدار
التسارع (m/s² 20, غربا)	متجهة	لأنها حددت بمقدار واتجاه
الشغل (J200)	قياسية	لأنها حددت فقط بمقدار
القوة (120N شمالاً)	متجهة	لأنها حددت بمقدار واتجاه

ملاحظات مهمة:

يمكن تمييز الكمية المتجهة عن القياسية بعدة طرائق منها:

• وضع سهم فوق رمز الكمية المتجهة مثل (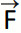) لتمييز متجه الفوة.
• يتم التعبير عن مقدار المتجه باستخدام القيمة المطلقة له | 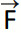| أو بكتابة (F) بدون السهم.
• ، يمكن التعبير عن الكمية المتجهة من خلال كتابة رمزها بالخط العريض (F) لتمييز متجه القوة وبالخط العادي للدلالة على مقدار المتجه مثل (F)

الكمية المتجهة:

المتجه ← أو F

مقدار المتجه ← | أو F.

سؤال: بالنسبة للكمية المتجهة الإشارة السالبة أو الموجبة تشير إلى اتجاه تلك الكمية، هل يمكن أن تكون الكمية القياسية سالبة؟

ج: الكمية القياسية تقبل دخول السالب إليها على عكس الكمية المتجهة فلا تقبل بل يتم التعبير عن السالب بالاتجاه. كمثال درجة الحرارة قد تكون سالبة وهي كمية قياسية والإشارة السالبة هنا لا تعني اتجاها.

سؤال: ما الفرق بين المسافة والإزاحة؟

الإجابة:

• المسافة: طول المسار الفعلي بين نقطتي البداية والنهاية.

المسافة كمية قياسية.

• الإزاحة: الخط المستقيم من نقطة البداية باتجاه نقطة النهاية.

الإزاحة كمية متجهة.

سؤال: هل يمكن أن يكون للكمية المتجهة والكمية القياسية الوحدة نفسها؟

ج: نعم كمثال المسافة (كمية قياسية) والإزاحة (كمية متجهة) ووحدة كل منهما (المتر).

سؤال: هل يمكن أن تتساوى كميتان متجهتان في المقدار وتختلفان في الاتجاه؟

ج: نعم يمكن؛ فمثلاً نقول تؤثر في الجسم قوتان متساويتان في المقدار إحداهما باتجاه الشرق والأخرى باتجاه الشمال فهنا الكميات المتجهة تساوت في المقدار واختلفت في الاتجاه ويمكن كذلك أن تكون الكميات المتجهة مختلفة في المقدار ومتماثلة في الاتجاه.

سؤال: في أثناء جلوسك في الغرفة الصفية سقط قلم باتجاه سطح الأرض. حدد كميتين قياسيتين وكميتين متجهتين تتعلق بهده الحادثة؟

الإجابة:

• الكميات القياسية: كتلة القلم، زمن سقوط القلم، درجة حرارة الغرفة الصفية.
• الكميات المتجهة: وزن القلم (نحو الأسفل دائما)، سرعة سقوط القلم (نحو الأسفل).

سؤال: ما هو الفرق بين الكتلة والوزن؟

الإجابة:

• الكتلة: هي تعبير عن كمية المادة بالجسم وهي كمية قياسية وتقاس بوحدة (الكيلوغرام).
• الوزن: هو القوة الناتجة عن سحب الجاذبية لجسم ما بمقدار معين، وينتج الوزن من تسارع الجاذبية وغالبًا ما يرمز للوزن برمز (w) وهي كمية متجهة لوجود اتجاه ومقدار لها، إذ يكون دائما اتجاهها بشكل عمودي نحو الأسفل.

كما أن وحدة قياس الوزن، هي ذاتها وحدة قياس القوة، إذ أن الوزن هو قوة السحب التي تجذب ال الأجسام لأسفل، نحو مركز الأرض، كما يرتبط وزن جسم ما بشكل مباشر بمقدار كتلته، أي أن الزيادة في الكتلة، ستؤدي لزيادة في الوزن…. وهكذا، فإن الوزن، هو مقياس للكتلة.

الوزن = الكتلة X تسارع الجاذبية

W=m x g

ملاحظات مهمة عن تمثيل المتجهات بيانيًا:

• التعامل مع الكميات القياسية وإجراء العمليات الحسابية عليها من جمع وطرح وضرب وقسمة أسهل من التعامل مع الكميات المتجهة.
• من السهل المقارنة بين كميتين قياسيتين خلافا للمقارنة بين متجهين وذلك لكل من المتجهين مقدارًا واتجاها لذلك نلجأ أحيانا لتمثيل الكميات المتجهة تمثيلا بيانيًا لتسهيل التعامل معها.
• يحدد مقدار الكمية المتجهة بعدد ووحدة قياس ولها اتجاه أيضا.

كيف يمكننا تمثيل المتجه بيانيا؟

الإجابة:

• نختار مستوى إحداثي مثل (x – y) ونقطة إسناد مثل نقطة الأصل (0،0).
• نرسم سهما بحيث يقع ذيله (نقطة بدايته) عند نقطة الأصل.
• طول السهم يمثل قيمة المتجه ويحدد باستخدام مقياس رسم مناسب.
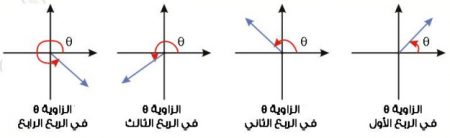
• اتجاه السهم يحدد نسبة إلى اتجاه مرجعي إما:

1. جغرافيًا باستخدام الجهات الأربعة (شمال، جنوب، شرق، غرب).
2. أو باستخدام الزاوية (θ) التي يصنعها المتجه مع المحور المرجعي.

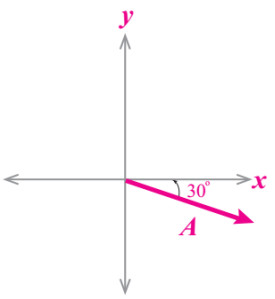
كمثال المتجه (A) في الشكل الآتي يكتب بصورة (درجة A =A,60) والتي تعني أن المتجه يصنع زاوية مقدارها (درجة 60) مع محور (x+).

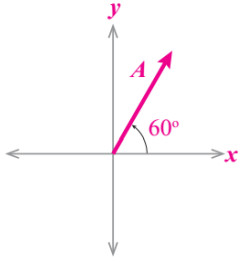
لاحظ أن طول السهم يعبر عن مقدار المتجه (A) وبالوضع الطبيعي يكون المحور المرجعي هو (x+)

مراجعة بسيطة للاتجاهات في الرسم الديكارتي

مراجعة بسيطة لمفهوم المحور المرجعي والزاوية المرجعية

تقاس الزاوية بالنسبة الى اتجاه مرجعي “محور إسناد” وهو محور السينات الموجب (x+) إلا إذا تم تحديد عكس ذلك في السؤال في حالات خاصة كما سنأتي على ذكرها لاحقا.

زاوية المرجع: هي الزاوية المحصورة بين ضلع انتهاء الزاوية ومحور السينات.

الشكل العام للتعبير عن المتجهات:

Vector = Magnitude + Unit, Angle

• زاوية المتجه: Angle.
• الوحدة: Unit.
• مقدار المتجه: Magnitude.
• المتجه: Vector.

Ex: (v=3 m/s, 270°), (F = 3 N, 45°), (a = 3 m/s², 45°)

بإمكاننا وضع الاتجاه بدلًا من الزاوية مثل (يمين، شمال شرق غرب،…..) أو نكتب أسم المحور مثلا (x+) أو (y-) وهكذا.. وهو نفسه dعبر عن الزاوية!

كمثال لو قلنا بأن الاتجاه نحو الشمال يعني أن المتجه يصنع زاوية (90) مع محور (x+).

اختيار مقياس الرسم المناسب

في تمثيل المتجهات نحتاج لاختيار مقياس الرسم المناسب لتحديد طول المتجه المناسب في الرسم، ويتم تقديره بما هو مناسب من قبل الطالب.

يتم التعبير عن طول المتجه في الرسم البياني بالوحدات كمثال طول السهم الذي يعبر عن مقدار المتجه 7 وحدات أو 10 وحدات وهكذا…

(cm1: Number + unit)

• وحدة الكمية الفيزيائية: unit
• قيمة الكمية الفيزيائية المناسبة لكل 1 سم: Number

بمعنى أن كل (cm1) من الرسم البياني على الورقة يمثل (مقدار) من الوحدة الفيزيائية.

سؤال: جِد مقياس الرسم المناسب للكميات الفيزيائية الآتية:

•  m/s 7 ← نختار مقياس رسم (1cm: 1 m/s): ج:

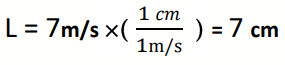
أي أن كل (1cm) على الورقة يمثل (1m/s) فيكون طول السهم على الورقة (7cm).

• 60N ← نختار مقياس رسم 10N) :1cm). ج:

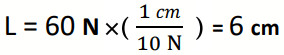
أي أن لكل (cm1) على الورقة يمثل (10N) فيكون طول السهم عالورقة (cm 6).

يستطيع الطالب حل السؤال بأكثر من طريقة مناسبة من خلال تقدير الطول المناسب للمقياس مثلا لنعتبر أنني أخترت مقياس الرسم (1cm:6N) يعني أن كل (cm 1) على الورقة يُمثل (6N) فيكون بذلك طول السهم على الورقة (cm 10).

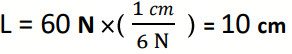
•  m/s 120 ← نختار مقياس رسم (1cm: 20 m/s). ج:

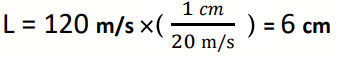
أي أن كل (cm 1) على الورقة يمثل (20m/s) فيكون طول السهم على الورقة (cm 6).

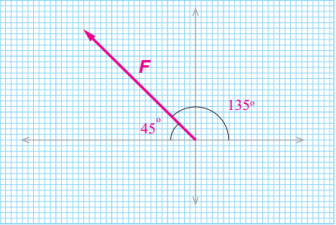
سؤال: توثر قوة (F) مقدارها (40N)، باتجاه يصنع زاوية مقدارها (°45)، مثل متجه القوة (F) بيانيا.

الإجابة:

نختار مقياس رسم مناسب وليكن (cm1: N10): أي أن كل (cm1) على الورقة يمثل (10N) فيكون طول السهم:

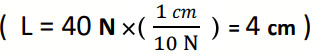
فنرسم سهما طوله (cm 4) وله نقطة بداية عند نقطة الأصل بحيث يصنع زاوية مقدارها (°45) مع محور السينات الموجب (المحور المرجعي).

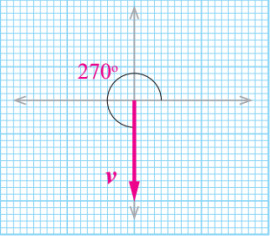
سؤال: اكتسب جسم سرعة (°270 m/s =)، مثل متجه السرعة بيانيا:

الإجابة:

نختار مقياس رسم مناسب وليكن: 1cm : 1m/s أي أن كل (1cm) على الورقة يمثل (1m/s)

فيكون طول السهم: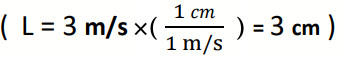

فنرسم سهما طوله (3cm) وله نقطة بداية عد نقطة الأصل بحيث يصنع زاوية مقدارها (°270) مع محور السينات الموجب (المحور المرجعي).

تحديد مكان الزاوية المرجعية في حالة تغير المحور المرجعي الخاص بها:

لو قلنا أن هنالك متجه صنع زاوية (°370) أو (°60) كمثال فبكل بساطة نقوم برسم الزاوية مع محور السيات الموجب ونحدد طول سهم المتجه من خلال مقياس الرسم المناسب ونرسم.

لكن ماذا نفعل لو قال لنا في السؤال أن الجسم صنع زاوية مقدارها كذا وكذا شمال الغرب أو جنوب الشمال وهكذا؟؟ كيف يمكننا التأكد بأن الزاوية مصنوعة مع المحور المرجعي وليست مع محور أخر؟

هنا نعتمد فرض أن الزاوية مصنوعة بين المتجه والمحور الذي فيه ال التعريف.

سؤال: حدد الزاوية المرجعية في الرسم للمتجهات في الحالات الآتية؟

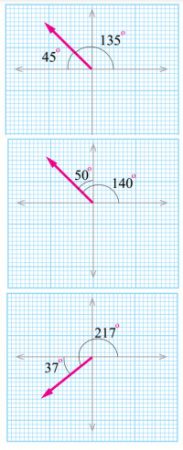
الإجابة:

(1) متجه يصنع زاوية (°45) شمال الغرب: يعني أنه بدأ من الغرب باتجاه الشمال وقطع زاوية (°45) أو بالأحرى الزاوية مصنوعة بين المتجه والمحور الذي فيه ال التعريف وهو الغرب في حالتنا هذه.

(2) متجه يصنع زاوية (°50) غرب الشمال: يعني أنه بدأ من الشمال باتجاه الغرب وقطع زاوية (°50) أو بالأحرى الزاوية مصنوعة بين المتجه والمحور الذي فيه ال التعريف وهو الشمال في حالتنا هذه.

(3) متجه يصنع زاوية (°37) جنوب الغرب: يعني أنه بدأ من الغرب باتجاه الجنوب وقطع زاوية (°37) أو بالأحرى الزاوية مصنوعة بين المتجه والمحور الذي فيه ال التعريف وهو الغرب في حالتنا هذه.

يمثل الشكل التالي الزوايا الرئيسية في الرسم البياني المطلوب من الطالب معرفتها ومعرفة موقعها ليتمكن بكل سهولة من إيجاد ومعرفة الزاوية المرجعية وقيمتها وأنتبه دائما تكون الزاوية المرجعية الصحيحة مصنوعة مع محور السينات الموجب.

سؤال: تؤثر قوة (F) مقدارها (60N)، باتجاه يصنع زاوية مقدارها (°45) شمال الغرب، مثل متجه القوة (F) بيانياً؟

الإجابة:

نختار مقياس رسم مناسب وليكن (cm1: N10) أي أن كل (cm1) على الورقة يمثل (10N) فيكون طول السهم:

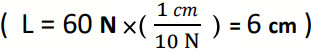
بما أن اتجاه المتجه يصنع زاوية مع شمال الغرب فذلك يعني أنه بدأ من الغرب باتجاه الشمال وقطع زاوية (°45) أو بالأحرى الزاوية مصنوعة بين المتجه والمحور الذي فيه ال التعريف وهو الغرب في حالتنا هذه، فنرسم سهما طوله (6cm) يصنع زاوية (°135) مع محور (x+).

سؤال: تسير سيارة بسرعة (v) مقدارها (80km/h)، في اتجاه يصنع زاوية مقدارها (°37) جنوب الشرق، مثل متجه القوة (٧) بيانيًا.

الإجابة:

نختار مقياس رسم مناسب مثل (1cm: 10 km/h) أي أن كل (cm1) على الورقة يمثل (10N) فيكون طول السهم:

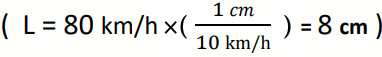
بما ان اتجاه المتجه يصنع زاوية مع شمال الغرب فذلك يعني أن الزاوية مصنوعة بين المتجه والمحور الذي فيه ال التعريف وهو الغرب في حالتنا هذه، فنرسم سهما طوله (cm8) يصنع زاوية (°37) مع محور (x+).

سؤال: استخدم معاذ (مش أنا * *) مقياس الرسم (1cm: 100m) لتمثيل متجه بعد المدرسة عن منزله (A)، إذا علمت أن طول سهم المتجه على الورقة يبلغ (5cm) فما هو بعد المدرسة عن منزل معاذ؟

الحل:

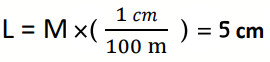
طول السهم ←L، بعد المدرسة عن منزل معاذ ( مقدار المتجه) ← M.

بعد المدرسة عن منزل معاذ = 500m، باتجاه يصنع زاوية (°65) مع شمال الشرق أو بدونها.

سؤال: استخدم احمد مقياس الرسم (1cm:20m) لرسم متجه يمثل بعد المسجد عن منزله (A)، حدد بعد المسجد عن منزل احمد مبينا الاتجاه؟

الإجابة:

في السؤال لم يحدد لنا طول السهم حتى نستخدم مقياس الرسم الموجود ونحدد البعد، لذلك نلجأ لاستخدام الأساليب الرياضية للبحث عن طريقة لإيجاد طول السهم:

نستخدم نظرية فيتاغورس لتحديد طول السهم (الوتر):

(طول السهم)² = (2)² + (4)² = 20، طول السهم =

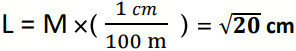
طول السهم ← L، بعد المدرسة عن منزل احمد ←M

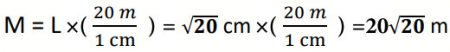
بعد المسجد عن منزل احمد =

لتحديد الاتجاه نحتاج لمعرفة الزاوية ← نستخدم قوانين المقابل والمجاور والزوايا ← (θ)tan:

بعد المسجد عن منزل أحمد = شمال الغرب.

سؤال: كيف يمكن تحديد كل من طول السهم واتجاهه عند تمثيل المتجه بيانيًا؟

ج: من خلال تحديد مقياس رسم مناسب لتحديد طول السهم على الورق وتحديد الزاوية بين المتجه والمحور المرجعي (x+) ورسمها في الرسم البياني.

خصائص المتجهات

• تساوي المتجهين.
• سالب معكوس المتجه.
• ضرب المتجه بكمية قياسية.

تساوي المتجهين:

← يتساوى المتجهان عندما يكون لهما المقدار والاتجاه نفساهما.

← يمكن نقل المتجه من مكان إلى آخر بشرط المحافظة على ثبات كل من مقداره واتجاهه.

سالب معكوس المتجه:

هو متجه له مقدار المتجه الأصلي ولكنه يعاكسه في الاتجاه أي أن الزاوية بين المتجه وسالب المتجه تساوي °180.

ضرب المتجه بكمية قياسية:

• يمكن ضرب متجه ما مثل (C) بكمية قياسية مثل n للحصول على متجه جديد (nC) مقداره (nC).
• يعتمد اتجاه المتجه (C) بعد ضربه بالكمية القياسية (nC) على إشارة (n):

← فإذا كانت موجبة فأن المتجه (nC) يكون في الاتجاه نفسه للمتجه (C). وإذا كانت سالبة فأن المتجه (nC) يكون عكس اتجاه للمتجه (C).

←من الأمثلة الفيزيائية على ضرب المتجه في كمية قياسية القانون الثاني لنيوتن، إذا أن محصلة القوى (ΣF) تساوي حاصل ضرب الكتلة (m) في متجه التسارع (a) بحسب العلاقة الآتية: ΣF = ma.

سؤال: وضح ما هو المقصود بكل مما يأتي:

• تساوي المتجهين: أي أن المتجهان لهما نفس المقدار والاتجاه.
• سالب المتجه: متجه له مقدار المتجه الأصلي نفسه ولكنه يعاكسه في الاتجاه.

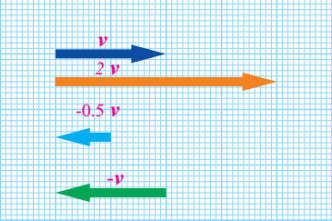
سؤال: تتحرك عربة بسرعة متجهة (۷) مقدارها 40m/s في اتجاه الشرق، مثل بيانيا:

1. متجه السرعة (٧).
2. المتجه (2v).
3. المتجه (0.5v-).
4. سالب المتجه (۷).

الإجابة:

أهم خطوة هي اختيار مقياس رسم بياني مناسب لتحديد طول السهم المناسب ورسمه، من خلال التقدير نستطيع اختيار مقياس 10m/s : 1cm) أي لكل (cm1) على الورقة يمثل (10m/s) فيكون طول السهم cm 4.

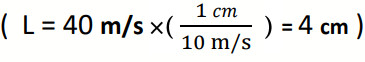
1. نرسم سهما طوله (4cm) ليمثل المتجه (۷) باتجاه الشرق كما في الشكل التالي.
2. نرسم سهما طوله (8cm) ليمثل المتجه (2v) ومقداره (80m/s) باتجاه الشرق.
3. نرسم سهما طوله (2cm) ليمثل المتجه   (0.5v-) ومقداره (20m/s) باتجاه الغرب.
4. نرسم سهما طوله (4cm) ليمثل المتجه (-v) ومقداره (40m/s) باتجاه الغرب.

سؤال: توثر قوة (F) مقدارها (250N) في جسم باتجاه يصنع زاوية مقدارها (°53) غرب الجنوب، مثل بيانياً؟

1. متجه القوة (F).
2. المتجه (F-)
3. المتجه (1.5F-).

الإجابة:

لتحديد طول السهم المناسب ورسمه، من خلال التقدير نستطيع اختيار مقياس رسم (N50 : 1cm) أي لكل (1cm) على الورقة يمثل N50 فيكون طول السهم 5cm.

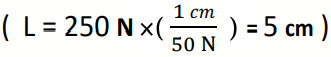
1. نرسم سهما طوله 5cm ليمثل المتجه (F) وبما ان اتجاه المتجه يصنع زاوية مع غرب الجنوب فذلك يعني أنه الزاوية مصنوعة بين المتجه والمحور الذي فيه ال التعريف وهو الجنوب في حالتنا هذه، فنرسم سهما طوله 5cm يصنع زاوية (°53) مع محور الجنوب.
2. نرسم سهمًا طوله 5cm ليمثل المتجه (F-)، المتجه الجديد يصنع زاوية مع شرق الشمال لأنه يمثل سالب المتجه فينعكس اتجاهه بمقدار (°180) يعني أن الزاوية مصنوعة بين المتجه والمحور الذي فيه ال التعريف وهو الشمال في حالتنا هذه، فنرسم سهما طوله (5cm) يصنع زاوية (°53) مع محور الشمال. (لاحظ الزوايا المتقابلة بالرأس متساوية).
3. نرسم سهما طوله (7.5mc) ليمثل المتجه (1.5F-)، المتجه الجديد يختلف في المقدار عن متجه (F) ويصنع زاوية مع شرق الشمال بسبب ضربه بسالب فتنعكس الاتجاهات فذلك يعني أن الزاوية مصنوعة بين المتجه والمحور الذي فيه ال التعريف وهو الشمال في حالتنا هذه، فنرسم سهما طوله (7.5cm) يصنع زاوية (°53) مع محور الشمال.

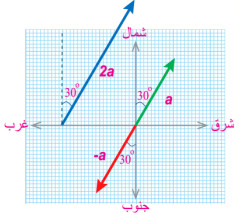
سؤال: تسير سيارة بتسارع ثابتm/s² 3) = a) في اتجاه يصنع زاوية مقدارها (°30) شرق الشمال، مثل بيانيا:

1) سالب المتجه (a)؟

2) ضرب المتجه (a) في الرقم 2؟

الحل:

لتحديد طول السهم المناسب ورسمه، من خلال التقدير نستطيع اختيار مقياس رسم 1m/s²: 1cm) أي كل (cm1) على الورقة يمثل (1m/s²) فيكون طول السهم cm 5.

ضرب المتجهات

كما شرحنا سابقا أن حاصل ضرب كمية قياسية في متجه ينتج عنه متجه، لكن ماذا لو احتجنا لضرب كمية متجهة في كمية متجهة أخرى فهل سيكون الناتج كمية متجهة أم قياسية؟

يمكن تقسيم أنواع ضرب المتجهات إلى:

1. الضرب القياسي.
2. الضرب المتجهي.

الضرب القياسي (النقطي): مقدار بدون اتجاه

• القانون الخاص بالضرب القياسي A.B = AB cosθ

حيث:

A ← مقدار المتجه (B (A ← مقدار المتجه (B).

θ ← الزاوية بين المتجهين (A) و (B) وتكون دائما بين (°0) و (°180).

• ينطلق المتجهان من النقطة نفسها.
• الناتج من عملية الضرب القياسي يكون كمية قياسية لها مقدار فقط، وهو مقدار يتغير بتغير مقدار الزاوية بين المتجهين.
• من التطبيقات الفيزيائية على الضرب القياسي الشغل (W) وهو حاصل الضرب القياسي لمتجه القوة (F) في متجه الإزاحة (d).

W = F.d = Fd cosθ

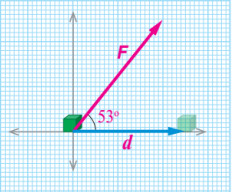
سؤال: أثرت قوة (F) مقدارها (120N) في جسم فحركته إزاحة (d) مقدارها (m 5) في اتجاه الشرق. فإذا علمت أن الشغل (W) الذي تنجزه القوة (F) يعطى بالعلاقة (W = F.d = Fd cosθ) وأن الزاوية بين اتجاه (F) واتجاه (d) مقدارها (°53) فأجيب عم يأتي:

1) مثل المتجهات (F) و (d) بيانياً؟

الحل:

اخترنا مقياس (cm1:m1) لتمثيل متجه (d) أي أن كل (cm1) على الورقة يمثل (m1) فيكون طول السهم 5cm ومقياس cm1:20N.

كل (cm1) على الورقة يمثل 20N فيكون طول السهم cm 6 يميل بزاوية (°53) عن متجه (d).

2) هل يعد الشغل (W) كمية متجهة؟ أوضح ذلك؟

الحل: لا، بل هو كمية قياسية؛ لأنه ناتج من الضرب القياسي لمتجهي القوة والإزاحة.

3) جد مقدار الشغل الذي أنجزته القوة؟

الحل:

ل 360 = W = F.d = F×d×cosθ = 120×5×cos (53°) = 120×5×0.6

الضرب المتجهي (التقاطعي ): مقدار و اتجاه

• القانون الخاص بالضرب المتجهي: A×B = AB sinθ

حيث:

A ← مقدار المتجه (B، (A – مقدار المتجه (B).

← الزاوية بين المتجهين (A) و (B) وتكون دائما بين (°0) و (°180).

• ينطلق المتجهان من النقطة نفسها.
• الناتج من عملية الضرب المتجهي يكون كمية لها مقدار واتجاه.
• لتحديد اتجاه حاصل الضرب المتجهي (A×B) نستخدم قاعدة كف اليد اليمنى.
• من التطبيقات الفيزيائية على الضرب المتجهي القوة المغناطيسية (F) المؤثرة على شحنة كهربائية (q) متحركة بسرعة (٧) في مجال مغناطيسي (B).

F = q(v×B) = q(vB sinθ)

وكذلك عزم القوة (T) يعطى بالضرب المتجهي بين القوة المؤثرة ومتجه الموقع.

T = (r×F)

شرح قاعدة كف اليد اليمنى

لو أردنا تحديد اتجاه (A×B) في الشكل الآتي…

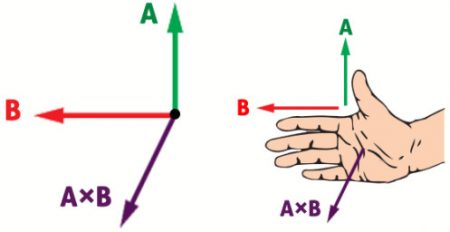
يشير اتجاه الإيهام إلى اتجاه المتجه الأول (A) وتشير الأصابع إلى اتجاه المتجه الثاني (B) فيكون اتجاه المتجه الناتج من خاصل ضربهما المتجهي (A×B) سهم خارج من كف اليد نحو محور (z+) (خارج من الورقة).

سؤال: ما الفرق بين الضرب المتجهي والضرب القياسي؟

الإجابة:

ناتج الضرب المتجهي يكون كمية متجهة لها مقدار واتجاه على عكس ناتج الضرب القياسي الذي يكون كمية قياسية لها مقدار فقط بدون اتجاه.

وفي قانون الضرب المتجهي تضرب مقدار المتجهين جيب الزاوية (sinθ) أما الضرب القياسي فنضرب مقدار المتجهين بجيب تمام (جتا) الزاوية (cosθ).

• يجب على الطالب معرفة الجهات وتحديدها في الرسم البياني:

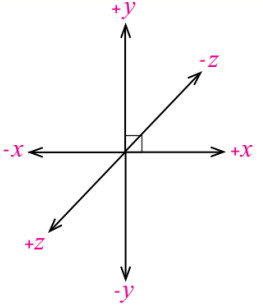
خارج من الورقة ← z+

داخل إلى الورقة ← z–

سؤال: في الشكل الآتي، إذا كان:

(F=250N) ، (r=0,4m) فأجيب عما يأتي:

1) جد مقدار عزم القوة (F)؟

الحل:

T = (r × F) = r × F × sinθ = 0.4 × 250 × sin90°

T = (r × F) = 100 N.m

بحسب قاعدة كف اليد اليمنى يشير الإيهام إلى اتجاه (r) وتشير الأصابع إلى اتجاه (F) لذا يكون اتجاه عزم القوة خارج من الورقة (باتجاه محور z+)

2) إذا تغيرت الزاوية بين (F) و (۲) لتصبح (°135) فما مقدار (F×r) واتجاهه؟

الحل:

sin 135° = 0.7

T = (F × r) = F × r× sinθ = 250 ×0.4 × sin 135° = 70 N.m

بحسب قاعدة كف اليد اليمنى يشير الإيهام إلى اتجاه (F) وتشير الأصابع إلى اتجاه (r) لذا يكون اتجاه عزم القوة خارج من الورقة (باتجاه محور z+).

سؤال: متجهان (A) و (B) مقدار كل منهما (20) فجد مقدار الزاوية بين المتجهين في الحالتين الأتيتين:

A.B = 320→ A × B × cos (θ) = 320 → (20) × (20) × cos (θ) = 320

cos (θ) = 0.8 → θ = 37°

1) A × B = 200 → A × B × sin (θ) = 200 → (20)×(20) × sin (θ) = 200

  → sin (θ) = 0.5

30° = θ

ملاحظات مهمة:

• في حال قمنا بعكس المتجهات في الضرب المتجهي (A×B) ليصبح (B×A) فإن مقدار المتجه يبقى نفسه لكن يختلف اتجاه المتجه المحصل.

إذا استخدمنا اليد اليسرى بدلًا من اليمنى لتحديد اتجاه المتجه المحصل الناتج من الضرب المتجهي فإن اتجاه المتجه ينعكس يعني كمثال لو كان الاتجاه عند استخدام اليد اليمنى هو ( z+) فإنه يصبح عند استخدام اليد اليسرى (z– ) وهكذا.

حل أسئلة مراجعة الدرس الأول من الوحدة الأولى

سؤال 1: أذكر اختلافا واحدًا بين:

• الكمية المتجهة والكمية القياسية:

ج: الكمية المتجهة لها مقدار واتجاه على عكس الكمية القياسية تكون مقدار بدون اتجاه.

• المتجه وسالب المتجه:

ج: سالب المتجه يكون عكس اتجاه المتجه أي أن الزاوية بينهما تكون (180) درجة.

• الضرب القياسي والضرب المتجهي:

ج: ناتج الضرب المتجهي يكون كمية متجهة لها مقدار واتجاه على عكس ناتج الضرب القياسي الذي يكون كمية قياسية لها مقدار فقط بدون اتجاه.

سؤال 2: صنف الكميات الآتية إلى متجهة وقياسية:

• زمن الحصة الصفية ← كمية قياسية.
• قوة الجاذبية الأرضية ← كمية متجهة.
• المقاومة الكهربائية ← كمية قياسية.
• درجة حرارة المريض ← كمية قياسية.
• كتلة حقيبتك المدرسية ← كمية قياسية.

سؤال 3: مثل بيانيًا الكميتين المتجهتين الآتيتين:

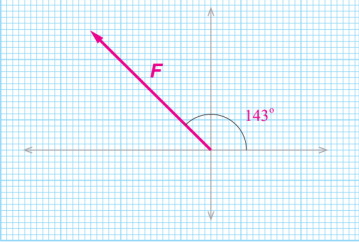
1. قوة مغناطيسية مقدارها (0.25N) في اتجاه يصنع زاوية مقدارها (°143) مع محور (x+):

الحل:

نختار مقياس رسم مناسب مثل: (1cm : 0.05N)K أي أن لكل (1cm) على الورقة يمثل (0.05N)K فيكون طول السهم:

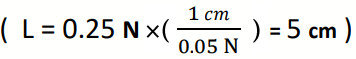
فنرسم سهما طوله (5cm) يصنع زاوية (°143) مع محور (x+).

2. تسارع ثابت مقداره (4m/s²) في اتجاه يصنع زاوية مقدارها (°30) جنوب الشرق:

الحل:

نختار مقياس رسم مناسب مثل (1cm:1m/s²) أي أن لكل (cm1) على الورقة يمثل (1m/s²) فيكون طول السهم:

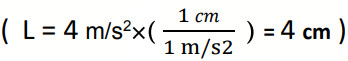
بما ان اتجاه المتجه يصنع زاوية مع جنوب الشرق فذلك يعني أن الزاوية مصنوعة بين المتجه والمحور الذي فيه ال التعريف وهو الشرق في حالتنا هذه، فنرسم سهمًا طوله (4cm) يصنع زاوية (°30) مع محور الشرق (x+).

سؤال 4: ما مقدار الزاوية بين الكميتين المتجهتين (F) و (L) في الحالات الآتية:

a) F × L = 0

F x L = 0 → FL sin (θ) = 0 → sin (θ) = 0 → θ = 0°, 180°

b) F.L = 0

F.L = 0 → FL cos(θ) = 0 → cos (θ) = 0 → θ = 90°, 270°

سؤال 5: اعتمادًا على العلاقة الآتية للتدفق المغناطيسي (Φ) ← Φ = B.A

احسب مقدار التدفق المغناطيسي (Φ) عندما تكون B = 0.1 Tesla)، ( A= 2×10⁻⁶ Tesla)) ومقدار الزاوية بين المتجهين (A) و (B) (45°)؟

الحل:

Φ = B.A = BA cos (θ) = (0.1) × (2 × 10⁻⁶) × cos (45°) = 2 x 10⁻⁷ × 0.707 = 1.414 × 10⁻⁷

سؤال 6: اعتمادًا على البيانات في الشكل المقابل، احسب مقدار حاصل الضرب المتجهي (B × A)، محددًا الاتجاه؟

الحل:

=(BxA)

  BA sineθ = 8 × 3 × sin90° = 24 unit

بحسب قاعدة كف اليد اليمنى يشير الإيهام إلى اتجاه (B) وتشير الأصابع إلى اتجاه (A) لذا يكون المتجه خارج نحو الغرب باتجاه محور (x -).

سؤال 7: سيارة تسير بسرعة ثابتة (v) وفي اتجاه محدد، وقد مثلث سرعة السيارة بيانيًا برسم سهم طوله (5cm) باستخدام مقياس الرسم (1cm:10m/s) على النحو المبين في الشكل المقابل، احسب مقدار سرعة السيارة محددًا اتجاهها?

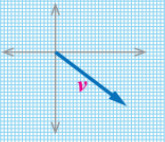
الحل:

طول السهم ← L

نقوم بضرب طول السهم بمقياس الرسم لإيجاد مقدار المتجه

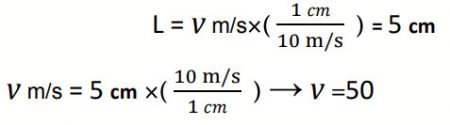
50= v نحو جنوب الشرق أو شرق الجنوب

سؤال 8: احسب مقدار الزاوية بين المتجهين (r) و (F) التي يتساوى عندها مقدار الضرب القياسي ومقدار الضرب المتجهي للمتجهين: r×F = r.F؟

الحل:

r×F = rF sin (θ), r.F = rF cos (θ)

 → rxF = r.F

°rF sin (θ) = rF cos (θ) → sin (θ) = cos (θ) → θ = 45