بطاقة الدرس:
- عنوانه: الحركة في بعدين
- ترتيبه: الثاني من الوحدة الثانية «الحركة».
- مادة: الفيزياء.
- الصف: العاشر الأساسي.
- الفصل الدراسي: الأول.
- المدارس: الأردنية.
- الهدف: شرح وتلخيص/مراجعة وحل أسئلة.
- الدرس السابق: الحركة في بعد واحد
سنتوسع في هذا الدرس لشرح مفهوم حركة الأجسام في بعدين وسنتعرف على عدة أنواع من الحركة في بعدين منها حركة المقذوفات والحركة الدائرية.
في الدرس الماضي تعلمنا كيفية وصف حركة الأجسام في بعد واحد والتعبير عن اتجاه كل من الإزاحة والسرعة والتسارع في بعد واحد. (حركة إما أفقية أو عمودية)
- نميزها بإشارة (+) إذا كانت الحركة نحو اليمين أو الأعلى.
- نميزها بإشارة (-) إذا كانت الحركة نحو اليسار أو الأسفل.
مفهوم الحركة في بعدين والمركبات المتعامدة
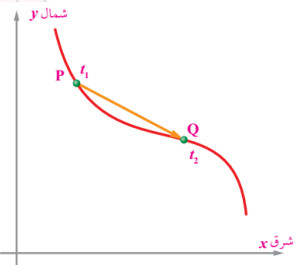
يبين الشكل طريقا أفقيًا متعرجا تسير عليه دراجة لنفرض أن الدراجة تحركت من الموقع (P) إلى الموقع (Q) على المسار المنحنى خلال مدة زمنية (Δt).
يمكن وصف هذه الحركة باستخدام مفاهيم الإزاحة والسرعة و التسارع لكن في بعدين لأن التغير يكون على المحور الأفقي والعمودي في نفس الوقت.
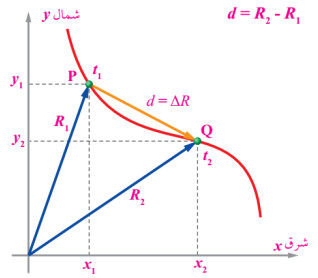
الشكل يبين شكل متجه الموقع الأول (R1) ومتجه الموقع الثاني (R2) وتم تحديدهم بالنسبة لنقطة مرجعية (0،0).
لاحظ أنه يمكن تفكيك متجه الموقعين إلى مركبتين من حركتين متعامدتين مركبة أفقية ومركبة عمودية مستقلتين تمامًا فالحركة العمودية (الرأسية) تخضع لقوة الجاذبية الأرضية بينما الحركة الأفقية لا تخضع لها.
- متجه الموقع الأول (R1) ← مركبة أفقية (x1) وعمودية (y1).
- متجه الموقع الأول (R2) ← مركبة أفقية (x2) وعمودية (y2).
التغير في الموقع (d) يمثله المتجه (d=ΔR)
ملخص الحكاية: سنحلل الحركة في بعدين إلى مركبتين إحداهما على محور (x) مركبة أفقية والأخرى على محور (y) مركبة عمودية (رأسية) لغرض وصف حركة الجسم.
كمثال يمكن تمثيل السرعة المتجهة للدراجة كالآتي:
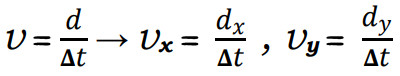
ملاحظات مهمة:
- حركة الجسم في مسار منحنى تدل على أن الحركة في بعدين وعند حركة الجسم في بعدين تتغير احداثيات حركته على المحورين الأفقي والعمودي (الرأسي) في اللحظة نفسها.
على عكس الحركة في بعد واحد يكون إما متحركا يمينا أو يسارًا أو نحو الأعلى أو الأسفل يعني فقط تتغير الحركة على محور واحد.
المقذوفات في بعدين:
الحالة الأولى ← قذف الجسم في اتجاه عمودي:
عند قذف جسم في اتجاه يصنع زاوية مع الأفق (السطح) فإنه يتحرك في مسار منحن (حركة في بعدين) بحيث تتغير إحداثيات حركة الجسم على المحورين الأفقي والرأسي في اللحظة نفسها.
حركة في بعدين ← مركبة أفقية وعمودية للمتجه.
نطبق معادلات الحركة الثلاثة في حالة الحركة في بعدين بحيث يكون هنالك معادلات للمحور الأفقي ومعادلات للمحور الرأسي بصورة مستقلة عن بعض.
يمكن تحليل سرعة الجسم المقذوف إلى مركبتين في أي موقع من المواقع التي يمر بها عبر مساره كمثال عند تحليل السرعة الابتدائية السرعة التي انطلق بها الجسم (Vo).
ملاحظات مهمة:
- في أثناء حركة الجسم المقذوف كما في السابق تكون المركبة الأفقية للسرعة ثابتة المقدار والاتجاه لأن التسارع الأفقي يساوي صغرًا (0 = ax) على عكس المركبة العمودية للسرعة التي تزداد إلى أن تصل لأقصى ارتفاع ثم تقل إلى أن تصل لسطح الأرض.
- تستمر الكرة في حركتها بعد الانطلاق إلى أن تصل إلى أقصى ارتفاع (h) ثم تعود للأسفل.
- تعاملنا هنا فقط مع المركبة الرأسية (العمودية).
- في أثناء حركة الجسم المقذوف تتأثر المركبة الرأسية للسرعة بقوة الجاذبية الأرضية مما يؤدي لحركتها بتسارع الجاذبية (g) يتناقص مقدار المركبة الرأسية تدريجيا في مرحلة الصعود إلى أن يصل إلى الصفر عند أقصى ارتفاع ثم تزداد تدريجيا في مرحلة الهبوط.
ملاحظات مهمة:
- المركبة الرأسية للسرعة عند أقصى ارتفاع تساوي صفر (Vy = 0 m/s).
- في معادلات الحركة عند التعامل مع السقوط الحر أو الجسم المقذوف في جاذبية الأرض نقوم باعتبار (ax = 0)- (ay = – g).
- دائما عند تعويض المركبة العمودية للسرعة النهائية (Vy) في معادلات الحركة بدلًا من (V2) يرافقها تعويض المركبة العمودية للسرعة الابتدائية (Voy) بدلا من (Vo) ونفس الشيء عند تعويض المركبة الأفقية للسرعة.
المركبة الأفقية للسرعة النهائية → Vx .
المركبة العمودية للسرعة النهائية ← Vy.
السرعة النهائية ← V2.
Vo=V1 ← السرعة الابتدائية, Vox ← المركبة الأفقية للسرعة الابتدائية , Voy ← المركبة العمودية للسرعة الابتدائية.
المركبة الأفقية للتسارع ويساوي صفر في هذه الحالة ← ax , المركبة العمودية للتسارع ← ay , التسارع ← a.
الإزاحة الأفقية ← X , الإزاحة العمودية أو الرأسية ← y , الإزاحة ← d.

سؤال: وضح ما هو المقصود بزمن التحليق (T)؟
ج: هو الزمن الكلي لحركة الجسم المقذوف في الهواء. ويساوي مجموع زمني الصعود والهبوط.
أو ببساطة هو مقدار الزمن الذي استغرقه الجسم من لحظة قذفه حتى عودته إلى نفس المستوى.
زمن الصعود ← زمن تحليق الجسم المقذوف من مستوى انطلاقه لأقصى ارتفاع.
زمن الهبوط ← زمن هبوط الجسم المقذوف من اقصى ارتفاع إلى مستوى نزوله (نهايته).
ليس شرطا أن يكون زمن الصعود مساوي لزمن الهبوط!
سؤال: متى يكون زمن صعود الجسم المقذوف مساويًا لزمن الهبوط ومتى لا يكون مساويًا؟
ج: يعتمد ذلك على المستوى الأفقي الذي يعود إليه الجسم المقذوف عن مستوى الإطلاق فإذا كان مختلفا عن مستوى الإطلاق يختلف زمن الهبوط عن زمن الصعود وإذا عاد إلى نفس المستوى الذي انطلق منه يكون زمن الهبوط مساويًا لزمن الصعود.
T= 2tI.
T= 2th.
(tn) تمثل زمن الصعود و (t) تمثل زمن الهبوط ويكون زمن الصعود مساوي لزمن الهبوط عندما يكون لهما نفس المستوى الأفقي.
سؤال: وضح ما هو المقصود بالمدى الأفقي؟
ج: المدى الأفقي (R): أكبر إزاحة أفقية يصنعها المقذوف من نقطة انطلاقه إلى أن يعود إلى مستوى الإطلاق نفسه (سطح الأرض كمثال)… أو ببساطة هو مقدار المسافة التي قطعها الجسم المقذوف بين نقطة القذف ونقطة السقوط.
أتحقَّقُ: استنتج العوامل التي يعتمد عليها كل من: أقصى ارتفاع، زمن التحليق؟
الإجابة:
- زمن التحليق يعتمد على مقدار السرعة الابتدائية ومقدار الزاوية التي يصنعها متجه السرعة الابتدائية مع الأفق.
- أقصى ارتفاع يعتمد مقدار السرعة الابتدائية ومقدار الزاوية التي يصنعها متجه السرعة الابتدائية مع الأفق.
عند طلب إيجاد زمن التحليق أو أقصى ارتفاع نستعمل مركبة السرعة الرأسية في المعادلات وعند طلب إيجاد المدى الأفقي نستعمل مركبة السرعة الأفقية.
أتحقق: بناء على العلاقات السابقة، أستنتج العوامل التي يعتمد عليها المدى الأفقي للمقذوف؟
ج: مقدار السرعة الابتدائية ومقدار الزاوية التي يصنعها متجه السرعة الابتدائية مع الأفق.
تدريب؟ أطلقت كتائب القسم قذيفة صاروخية من سطح الأرض نحو مستوطنات الاحتلال الإسرائيلي بسرعة ابتدائية مركبتها الأفقية (100ms) ومركبتها العمودية ( 294m/s)، جد ما يلي:
- الزمن بالدقائق اللازم لوصول القذيفة إلى أقصى ارتفاع.
- مقدار السرعة النهائية للقذيفة الصاروخية محددًا اتجاهها.
- بعد مستوطنات الاحتلال الإسرائيلي عن نقطة إطلاق القذيفة.
تدريب؟ ركل لاعب كرة قدم بسرعة ابتدائية مركبتها الأفقية ( 30m/s)، في اتجاه يصنع زاوية (°30) مع العمودي على الأفق، بإهمال مقاومة الهواء جد ما يلي:
- a) زمن تحليق الكرة حتى تعود إلى سطح الأرض.
- b) المدى الأفقي للكرة.
المقذوفات في بعدين:
الحالة الثانية ← قذف الجسم في اتجاه أفقي:
إذا قمنا بقذف الجسم في اتجاه أفقي من مكان مرتفع عن سطح الأرض حيث (0=θ)، فإن مركبتي السرعة الابتدائية تكونان:
Vox = Vo cosθ = Vo x cos0 ° = Vo
0=°Voy = Vo sind θ= Vo × sin0
- نعوض الإزاحة (Y) سالب إذا كان اتجاه الإزاحة نحو الأسفل بعكس الاتجاه الموجب.
- زمن التحليق (T) في هذه الحالة يكون نفسه زمن الهبوط (t).
سؤال: ما الأثر المتوقع في حال عدم إهمال مقاومة الهواء لحركة الكرة على المركبتين الأفقية والرأسية للسرعة؟
ج: تتأثر المركبة الرأسية للسرعة بذلك بسبب وجود أثر إضافي إما معاكس لها أو في نفس جهتها.
تدريب؟ قذف “نيشان” حجر أفقيا من سطح منزله بسرعة ابتدائية مقدارها (5m/s)، فوصل الحجر إلى سطح الأرض بعد مرور (10s)، جد ما يلي:
- ارتفاع منزل “نيشان”.
- أكبر إزاحة أفقية يصنعها الحجر.
الحركة الدائرية المنتظمة
الدوران في مسار دائري أفقي بسرعة ثابتة المقدار ومتغيرة الاتجاه.
- يملك الجسم في الحركة الدائرية تسارعا مركزيا (ac).
- يكون اتجاه التسارع المركزي دائما نحو مركز الدوران.
- يؤدي التسارع المركزي لحدوث تغير في اتجاه السرعة. يتعامد دائما متجه التسارع المركزي مع متجه السرعة. يكون دائما متجه السرعة على امتداد مماس الدائرة (سرعة مماسية).
- مركز المسار الدائري يمثل نقطة إسناد مرجعية لتحديد المتغيرات.
سؤال: أعط أمثلة على الحركة الدائرية المنتظمة؟
ج: حركة نقطة مرسومة على طرف مروحة تدور، وحركة سيارة بسرعة ثابتة المقدار حول الدوار، وحركة بعض الأقمار الصناعية حول الأرض.
ملاحظات مهمة:
- السرعة عبارة عن طول المسار المقطوع على الزمن والمسار المقطوع هنا هو محيط الدائرة والزمن هنا هو الزمن الدوري (الزمن اللازم لإكمال دورة كاملة حول مركز الدوران).
- السرعة في حالة الحركة الدائرية المنتظمة تكون ثابتة المقدار متغيرة الاتجاه.
- السرعة القياسية المتوسطة تساوي السرعة القياسية اللحظية.
- السرعة القياسية المتوسطة تساوي السرعة القياسية اللحظية.
سؤال: | قمر صناعي يدور حول الأرض على ارتفاع (8420m) عن مركز الأرض، في مسار دائري تقريبا بسرعة مماسيه ثابتة المقدار كما في الشكل. إذا علمت أن الزمن الدوري له min (129) فجد ما يأتي:
- مقدار السرعة المماسية للقمر الصناعي:
الحل:

- التسارع المركزي لهذا القمر:
الحل:
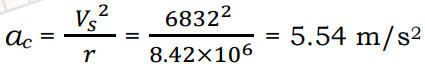
حل أسئلة مراجعة الدرس الثاني من الوحدة الثانية
سؤال: ما أهمية تحليل السرعة الابتدائية للمقذوفات إلى مركبتين أفقية ورأسية؟
ج: نقوم بتحليل مركبة السرعة الابتدائية لغايات وصف حركة الجسم ولاستعمال المركبتين في إيجاد زمن التحليق والمدى الأفقي والسرعة النهائية للجسم وأقصى ارتفاع.
سؤال: 2 أذكر مثالين من الحياة اليومية على حركة المقذوفات ومثالين آخرين على الحركة الدائرية المنتظمة.
الإجابة:
- حركة المقذوفات ← كرة السلة عند رميها من قبل اللاعب، ركل كرة القدم في الملعب.
- الحركة الدائرية المنتظمة ← حركة السيارة حول الدوار، دوران القمر الصناعي حول كوكب الأرض.
سؤال: فَسِّر ما سبب وجود تسارع مركزي وعدم وجود تسارع مماسي في الحركة الدائرية المنتظمة؟
ج: السرعة المماسية ثابتة المقدار وبالتالي التسارع المماسي يساوي صفرًا. على عكس السرعة المركزية.
سؤال: قارن بين مركبتي كل عنصر من العناصر الآتية لحركة المقذوفات الأفقية والرأسية؟
الإجابة:
- الإزاحة ← (x) في حالة الحركة على المحور الأفقي، و (y) في حالة الحركة على المحور العمودي.
- السرعة ← (Vx) في حالة الحركة على المحور الأفقي، و (Vy) في حالة الحركة على المحور العمودي.
- التسارع ← ( x ) في حالة الحركة على المحور الأفقي، و (g=ay) في حالة الحركة على المحور العمودي.
سؤال: | 5 قذفت كرة بسرعة مقدارها (15.8m/s) نحو الأعلى في اتجاه يصنع مع الأفق زاوية مقدارها (°30)، بإهمال مقاومة الهواء لحركة الكرة، جد:
- زمن تحليق الكرة:
الحل:
Vox = Vo cosθ = 15.8 × cos30° =13.6 m/s
Voy = Vo sinθ = 15.8 × sin30°=7.9 m/s
Vy= Voy -gt→0 = 7.9 -9.8x t→t =0.80 s
t=2xt = 2×0.80 = 1.60 s
أقصى ارتفاع للكرة:
الحل:
V2² = V1² + 2ad → (Vy)² = (Voy)² – 2gh → (Vy)² = (Voy sinθ)² – 2gh
(0²) = (7.9²)-2 × (9.8)× h ←h
= 3.184 m
⇐ درس مُقترح للمراجعة: جمع المتجهات وطرحها