سيدور ما لدينا هنا (درس / مقال معلوماتي) يتمحور حول الجاذبية الأرضية من حيث التعريف والتفصيل، ثم قانون الجذب العام؛ وأخيرًا سنُجيب على: كيف يُمكننا حساب تأثير الجاذبية الأرضية على جسم ما؟.. فلنُتابِع سويًا.
إذا نظرنا حولنا نُلاحظ أن كل شيء يسقط نحو الأرض حتى قطرات المطر بالرغم من صغر حجمها، وخفة وزنها، لا تبقى عائمة في الهواء بل تسقط على الأرض.
وإذا حاولتم القفز في الهواء سرعان ما تعودون إلى الأرض، فكل شيء يسقط باتجاه الأرض، وتحديدا نحو المركز.
إذا كان هناك حفرة في الأرض لا تسقط الأمطار على الأرض فقط، بل تسقط في الحفرة باتجاه مركز الأرض.
وإذا مسكتم علبة دبابيس ثم أفلتموها تقع الدبابيس على الأرض، وربما ترتطم في الأرض، وترتد في الهواء، لكن سرعان ما تسقط على الأرض ثانية.
تحدث هذه الأمور حولنا بشكل طبيعي دون أن تلفت الأنظار، لكن هذا الأمر لم يكن طبيعياً للعالم إسحاق نيوتن؛ الذي لفت نظره سقوط جميع الأجسام بشكل عموديٍ على الأرض، فاستنتج العديد من الأمور ووضع أسس في علم الفيزياء.
تعريف الجاذبية الأرضية ومعلومات عنها
يُعتبر العالِم إسحاق نيوتن من عباقرة العالَم؛ فعندما لاحظ سقوط الأجسام على الأرض سأل نفسه؛ لماذا تسقط الأجسام دوما نحو الأرض؟
ويقال أن ما لفت انتباهه هو سقوط تفاحة من الشجرة على الأرض أثناء جلوسه بالقرب منها.
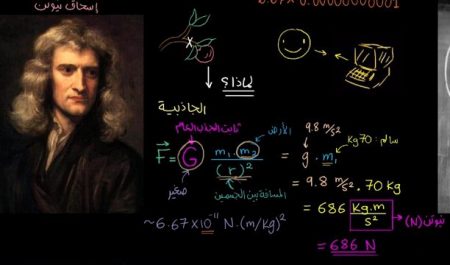
وتوضح هذه الصورة كل ما نقوله تفصيلاً وبالقوانين. فعندما لاحظ نيوتن سقوط التفاحة باتجاه الأرض بشكلٍ عموديٍ، سأل نفسه؛ لماذا سقطت التفاحة باتجاه الأرض؟
هذا السؤال عن أمر مألوف جداً كان حجر الأساس لقوانين الحركة الميكانيكية التي ما زالت تستخدم حتى يومنا هذا.
وقد أضاف إليها وعدل عليها عالم الفيزياء ألبرت أينشتاين في نظريته النسبية حين أضاف جمع بين الزمن والأبعاد الثلاثية في الفراغ فيما يُعرفُ بالزمكان أو الزمان المكاني Spacetime.
تفسير أينشتاين للجاذبية يرتبط عادة بسرعة الضوء، لكن حين يتعلق الأمر بما يجري بالقرب من سطح الأرض لا بد من العودة إلى قوانين نيوتن.
لم يكتفي نيوتن بالإشارة إلى وجود قوة تجذب التفاحة نحو الأرض، وتجعلها تسقط بشكلٍ عموديٍ بل وضع قانوناً يفسر قوة الجذب بين جميع الأجسام.
قانون الجذب العام
أطلق نيوتن على القوة التي تجذب الأجسام نحو الأرض عند سقوطها اسم الجانبية، ووضع بناء على ذلك “قانون الجذب العام” الذي ينص على أن (القوة بين جسمين ويرمز لها بحرف F أعلاه إشارة المتجه؛ لأنها كمية متجهة = قيمة ثابتة يرمز لها بحرف G كبير، وتسمى ب “ثابت الجذب العام” ضرب كتلة الجسم الأول m1 ضرب كتلة الجسم الثاني m2 تقسيم r تربيع، وهي المسافة بين الجسمين).
في حالة التفاحة فإن إحدى الجسمين هنا هو الأرض والجسم الآخر هو التفاحة، والمسافة تُقاس من مركز التفاحة إلى مركز الأرض.
ولاحظوا أن هذا القانون لا يشير فقط إلى أن أحد الجسمين فقط يؤثر بقوة جذب على الجسم الآخر؛ بل يشير إلى وجود قوة جذب بين أي جسمين في الكون.
بمعنى آخر عند الجلوس أمام حاسوب لا بد من وجود قوة جذب بين جهاز الحاسوب ومن يجلس أمامه. فكيف يبقى الجهاز في مكانه ولا يتحرك نحو من يجلس أمامه؟
ذكرنا في البداية أن ثابت الجذب العام صغير جداً، إذا هناك قوة جذب بين الحاسوب ومن يجلس أمامه. ولكن هذه القوة صغيرة جداً مقارنة بقوة الاحتكاك بين الحاسوب والطاولة، وبين الجالس أمام الحاسوب والكرسي، والناتج عن قوة جذب الأرض للجالس، وقوة جذب الأرض لجهاز الحاسوب.
وذلك لأن كتلة الحاسوب ومن يجلس أمامه صغيرة جداً، وبالتالي؛ قوة الجذب بينهما صغيرة، ويمكن إهمالها مقارنة بالقوى الأخرى، بالتالي؛ تبقى الأجسام في مكانها.
ثابت الجذب العام هذا يساوي تقريباً 6.67 × 10 أس سالب 11 نيوتن أم ضرب متر على كيلو جرام الكل تربيع.
ولاحظوا عند ضرب ثابت الجذب العام بالكتلة بوحدة الكيلوجرام وتقسيمه على مربع المسافة بوحدة المتر تُختصر جميع الوحدات، ويبقى نيوتن وهو وحدة قياس القوة.
ونُلاحظ أن هذا الرقم صغير جداً ف 10 أس سالب 11 تعني 11 منزلة عشرية بعد الفاصلة ضرب 6.67
لذلك عند ضربه بكتلة أجسام صغيرة نسبياً مثل جهاز الحاسوب، ومن يجلس أمامه؛ سيكون الناتج قوة مقدارها صغير جداً، لا يُمكنها التغلب على القوة الأخرى الأكبر مقداراً.
لكن لو كانت كتلة أحد الجسمين كبيرة مثل الأرض ستكون قوة الجذب كبيرة، ويمكن ملاحظة آثارها بسهولة مثل قوة الجانبية.
لذلك يمكن حساب قوة الجاذبية الأرضية بتعويض كتلة الأرض مكان m2 ومقدار المسافة بين مركز الأرض وسطح الأرض؛ أي نصف قطر الأرض هنا عند ضرب ثابت الجذب العام بكتلة الأرض على نصف قطر الأرض تربيع سيكون الناتج ما يُسمى بمجال الجاذبية الأرضية، ويُرمز لها بحرف g صغير، وهو ما يُعرف أيضاً بتسارع الجاذبية الأرضية، ويساوي تقريباً 9.8 متر في الثانية تربيع.
ندعوك هنا لتقرأ وتجِد: أسئلة وتمارين عن القوى المتوازنة وغير المتوازنة والقوى المحصلة
كيف يُمكننا حساب تأثير الجاذبية الأرضية على جسم ما؟
لحساب تأثير الجاذبية الأرضية على جسم ما يمكن ضرب تسارع الجاذبية هذا بكتلة الجسم m1.
إذاً كان الجسم قريباً من سطح الأرض، فإن قوة الجاذبية = تسارع الجاذبية × كتلة هذا الجسم.
فعلى سبيل المثال؛ لو كانت كتلة سالم 70 كيلو جرام فإن قوة جذب الأرض لسالم = 9.8 متر في الثانية تربيع × الكتلة 70 كيلوجرام. باستخدام الآلة الحاسبة 9.8 × 70 = 686.
قوة الجاذبية علي سالم = 686 كيلو جرام متر في الثانية تربيع.
هذه الوحدات معاً تُسمى نيوتن نسبة إلى العالم نيوتن، ويرمز لها ب الحرف N.
إذا قوة جذب الأرض لسالم هي ما يُشار إليه بالوزن؛ أي أن وزن سالم = 686 نيوتن حسب هذا المثال السابق.
وإذا كان سالم يقف في مكان ما على الأرض، فإن الأرض تجذبه نحو الأسفل بقوة مقدارها 686 نيوتن.
ماذا عن قوة جذب سالم للأرض؟ هل يجذب سالم الأرض بقوة أصغر أم أكبر من قوة جذب الأرض؟
بمعنى آخر؛ بما أن الأرض كبيرة جداً، وسالم صغير جداً بالنسبة لها، فهل هذا يعني أن قوة جذب الأرض أكبر بكثير من قوة جذب سالم لها حسب قانون الجذب العام تؤثر الأرض علي سالم بقوة جذب مقدارها 686 نيوتن، وسالم يؤثر على الأرض بقوة مقدارها 686 نيوتن؛ لأنه قانون الجذب العام ينُص على أن هناك قوة جذب بين الجسمين، ولكن كيف يُمكن تفسير ما يحدث عند سقوط الأجسام سقوطاً حراً؟
لو أمسك سالم بدمية وألقاها من مكان مرتفع تؤثر قوة الجاذبية على الدمية، فتتسارع نحو الأسفل. ولكن الأرض لن تتسارع نحو الأعلى باتجاه الدمية. عند سقوط الأجسام سقوطاً حراً تجذبها قوة الجاذبية نحو الأسفل، فتتسارع. هذه القوة F = الكتلة m × التسارع a.
إذا كانت كتلة الدمية = كتلة سالم فإن قوة جذب الأرض للدمية = 686 نيوتن، وتساوي 70 كيلو جرام ضرب التسارع.
إذا قسمنا الطرفين على 70 نجد أن التسارع = 9.8 متر في الثانية تربيع.
ولحساب مقدار تسارع الأرض نحو الدمية 686 نيوتن يساوي كتلة الأرض 5.972 × 10 أس 24 كيلو جرام ضرب التسارع.
وعند قسمة الطرفين على كتلة الأرض نجد أن التسارع = 1.15 × 10 أس سالب 22 وهو قيمة صغيرة جداً جداً لا يمكن ملاحظة أثرها مقارنة بقوة جذب الأرض. وينطبق هذا على كافة الأجسام على سطح الأرض، وهذا يفسر سقوط الأجسام نحو الأرض.
وفي النهاية نعرض صورة توضيحية على المثال السابق.

