بطاقة الدرس:
- عنوانه: الحركة في بعد واحد
- ترتيبه: الأول من الوحدة الثانية «الحركة».
- مادة: الفيزياء.
- الصف: العاشر الأساسي.
- الفصل الدراسي: الأول.
- المدارس: الأردنية.
- الهدف: شرح وتلخيص/مراجعة وحل أسئلة.
- الدرس السابق «والأخير من الوحدة الأولى»: جمع المتجهات وطرحها
تصنف أشكال الحركة ضمن ثلاثة مجالات رئيسية:
- الحركة في بعد واحد.
- الحركة في بعدين.
- الحركة في ثلاثة أبعاد.
الحركة في بعد واحد تعنى أن الجسم يتحرك في خط مستقيم بشكل أفقي على محور (x) أو بشكل عمودي أو رأسي على محور (y).
الإطار المرجعي للحركة
عند تحديد موقع جسم لوصف حالته الحركية فأننا نعتمد على جسم أخر قربه أو على نظام إحداثيات متعامدة ونقطة إسناد محددة.
الموقع والإزاحة
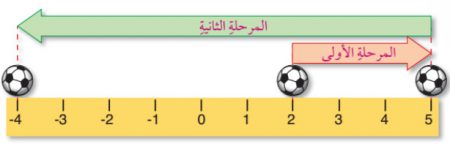
نعبر عن موقع الكرة في الشكل السابق بالنسبة إلى نقطة الإسناد (0=x):
- إذا كان موقع الكرة على يمين نقطة الإسناد تكون (x) موجبة.
- إذا كان موقع الكرة على يسار نقطة الإسناد تكون (x) سالبة.
يمكن وصف حركة الكرة في الشكل باستخدام مفهوم:
- الإزاحة: كمية متجهة.
- المسافة: كمية قياسية.
ملحوظة: التعويض في القوانين يكون بالوحدات الأساسية إلا إذا طلب العكس…
الإزاحة في الشكل فوق: الفرق بين متجه موقع الكرة النهائي (x2) ومتجه موقعها الابتدائي (x1) ويمكن التعبير عنها من خلال القانون الآتي:
ΔX = X2-X1
← في المرحلة الأولى انتقلت الكرة من الموقع ( x1=2 ) إلى الموقع ( x2=5) لذا تكون إزاحة الكرة في المرحلة الأولى:
X2-X1 =(ΔX)1
2-5=3+m
إشارة الإزاحة الموجبة تدل على أن الكرة تحركت في اتجاه محور (x) الموجب.
← في المرحلة الثانية انتقلت الكرة من الموقع ( x1=5 ) إلى الموقع (x2=-4) لذا تكون إزاحة الكرة في المرحلة الأولى:
Δx2=x2-x1=(-4)-(5)=-9m
إشارة الإزاحة السالبة تدل على أن الكرة تحركت في اتجاه محور (x) السالب.
يمكن حساب الإزاحة الكلية للكرة في المرحلتين الأولى والثانية من خلال حاصل جمع الإزاحتين للمرحلة الأولى والثانية:
Δx=(Δx)1+(Δx)2=(+3)+(-9)=-6m
أو يمكن حساب الإزاحة الكلية للكرة في المرحلتين الأولى والثانية مباشرة من خلال إيجاد الفرق بين موقعي الكرة الابتدائي والنهائي كما يأتي:
Δx=(Δx)1-(Δx)2=(-4)-(+2)=-6m
المسافة: كمية قياسية قيمتها تساوي طول المسار الفعلي الذي اتبعه الجسم ويرمز إليها بالرمز (s) ويمكن التعبير عنها من خلال القانون الآتي:
S = S1 + S2
المسافة الكلية التي قطعتها الكرة (s) هي المسافة التي قطعتها الكرة في المرحلة الأولى (S1= 3m) مضافا إليها المسافة التي قطعتها الكرة في المرحلة الثانية (S2 = 9 m).
S = S1 + S2 = 3 + 9 = 12 m
| الإزاحة كمية متجهة | المسافة كمية قياسية |
| تعتمد الإزاحة على موقعي الجسم الابتدائي والنهائي | تعتمد المسافة على طول المسار الفعلي للجسم. |
| الإزاحة موجبة (تشير إلى اتجاه اليمين والأعلى بالنسبة إلى نقطة الإسناد).
الإزاحة سالبة (تشير إلى اليسار والأسفل بالنسبة إلى نقطة الإسناد). |
المسافة تكون موجبة دائمًا. |
سؤال: فيم تختلف المسافة التي قطعتها الكرة عن الإزاحة التي أحدثتها الكرة في هذه الحركة؟ وأيهما أكبر المسافة أم مقدار الإزاحة؟
ج: المسافة طول المسار الفعلي المقطوع بين نقطة البداية والنهاية وهي كمية قياسية بينما الإزاحة هي الخط المستقيم الذي يصل بين نقطة البداية ونقطة النهاية وهي كمية متجهة. دائما المسافة أكبر من أو تساوي الإزاحة….
سؤال: بدأ معاذ الحركة من منزله باتجاه المسجد نحو الشمال فقطع مسافة (12m) ثم تحرك نحو الغرب باتجاه المدرسة فقطع مسافة (15m)، ثم تحرك نحو منزل صديقه ياسر باتجاه الجنوب فقطع مسافة (12m)، كم تبلغ المسافة الكلية والإزاحة التي قطعها معاذ للوصول لمنزل صديقه؟
الحل:
S = S1 + S2 + S3 = 12 + 15 + 12 = 39m
- المسافة الكلية المقطوعة = 39m.
- الإزاحة هي خط مستقيم يصل بين البداية والنهاية.
- الإزاحة = 15m-، وضعنا سالب لأن حركة معاذ نحو الغرب.
سؤال: فكر متى تتساوى المسافة مع مقدار الإزاحة؟
ج: عندما تكون حركة الجسم بخط مستقيم من نقطة البداية نحو نقطة النهاية.
تدريب؟ “عدو صهيوني” هارب من “مقاوم فلسطيني” باتجاه الشمال وبعد أن قطع مسافة (8km) وصل المركز الأمني فأمسك به المقاوم الفلسطيني وقام بطعنه ولاذ المقاوم بالفرار باتجاه الشرق فقطع مسافة (7m) إلى أن وصل إلى بر الأمان.
1) كم تبلغ المسافة الكلية والإزاحة التي قطعها “المقاوم الفلسطيني”؟
2) كم تبلغ المسافة الكلية والإزاحة التي قطعها “العدو الصهيوني” مع العلم بأنه فقد حياته عند موقع المركز الأمني بسبب الطعنة؟
السرعة
السرعة القياسية: مقدار معدل تغير المسافة المقطوعة بالنسبة للزمن. أو المسافة التي يقطعها الجسم في زمن معين بغض النظر عن اتجاه حركته.
السرعة المتجهة: معدل تغير الإزاحة المقطوعة بالنسبة للزمن
السرعة المتوسطة: من أهم مظاهر وصف حركة جسم ما السرعة التي يتحرك بها.
1) السرعة القياسية المتوسطة: تحسب من خلال قسمة المسافة الكلية التي يقطعها الجسم (المسافة) (S) على الزمن الكلي للحركة (Δt).
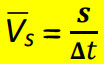
تقاس بوحدة (m/t)، وليس لها اتجاه لأن المسافة والزمن ليس لهما اتجاه.
2) السرعة المتجهة المتوسطة: السرعة المتجهة المتوسطة تحسب من خلال قسمة الإزاحة الكلية للجسم (الإزاحة) (Δx) على الزمن الكلي للحركة (Δt).
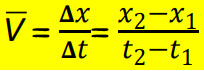
- تقاس بوحدة (m/t)، ولها اتجاه لأن الإزاحة لها اتجاه.
- اتجاه السرعة المتجهة يكون باتجاه الإزاحة.
الزمن ← t
الإزاحة ← x
المسافة المقطوعة ← S
سؤال: قطع فراس بدراجته مسافة (m 645) خلال مدة زمنية مقدارها (s 86). جد السرعة القياسية المتوسطة؟
الحل:
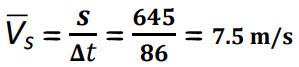
سؤال: قطع عز الدين بسيارته إزاحة مقدارها (m(500) نحو الجنوب خلال مدة زمنية مقدارها (100). جد السرعة المتجهة المتوسطة؟
الحل:
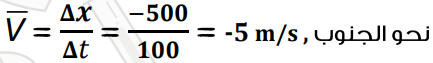
تدريب؟ تتحرك سيارة نحو الشرق بسرعة (15km/h)، كم استغرقت السيارة من الزمن بالثواني لقطع إزاحة مقدارها (1.5km)؟
السرعة المتجهة اللحظية
السرعة المتجهة اللحظية: (V)
سرعة الجسم عند لحظة معينة مع تحديد اتجاه حركة الجسم، أما إذا لم يطلب أو يحدد الاتجاه فأن فالمقدار يعبر عن سرعة قياسية لحظية.
ملاحظات مهمة:
- إذا كانت السرعة المتجهة أو القياسية اللحظية ثابتة فإنها تساوي السرعة القياسية أو المتجهة المتوسطة دائما.
- تكون حركة الجسم منتظمة إذا تحرك بسرعة قياسية ثابتة.
- في هذا الكتاب الجديد كلمة “سرعة” تدل دائما على السرعة المتجهة إلا إذا حدد عكس ذلك في السؤال.
سؤال: ما الشرط الواجب توافره في الحركة في بعد واحد لكي تتساوي السرعة المتجهة المتوسطة مع السرعة اللحظية؟
ج: إذا كانت السرعة المتجهة أو القياسية اللحظية ثابتة فإنها تساوي السرعة القياسية المتوسطة أو المتجهة المتوسطة دائما.
السرعة المتجهة: (في بعد واحد)
- موجبة ← حركة أفقية في اتجاه محور (x+) أو حركة عمودية في اتجاه محور (y+).
- سالبة ← حركة أفقية في اتجاه محور (x-) أو حركة عمودية في اتجاه محور (y-).
سؤال: وضعت لعبة سيارة على محور ( x ) على بعد (2m) من نقطة الأصل في الاتجاه الموجب، ثم حركت في الاتجاه الموجب فأصبحت على بعد (6.8m) على المحور نفسه، ثم حركت في الاتجاه السالب فأصبحت على بعد (5.6m) كما في الشكل. إذا علمت أن الزمن الكلي للحركة هو (15s) فجد:
1) المسافة الكلية التي قطعتها لعبة السيارة:
الحل:
S = S1 + S2 = (2→6.8) + (6.8→5.6) = 4.8 + 1.2=6m
2) الإزاحة الكلية للعبة السيارة:
الحل:
X = X2-X1 = (5.6) – (2) = 3.6 m
3) السرعة القياسية المتوسطة للعبة السيارة:
الحل:
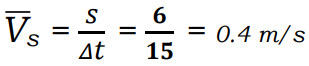
4) السرعة المتجهة المتوسطة للعبة السيارة:
الحل:
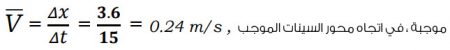
تدريب؟ في السؤال السابق لو وضعنا لعبة السيارة على محور (x) على بعد (1m) من نقطة الأصل، مع بقاء باقي المعطيات كما هي في السؤال، كم تصبح السرعة القياسية المتوسطة للعبة السيارة؟
التسارع الثابت
يمكن توضيح مفهوم التسارع بأنه حدوت تغير إما ازدياد أو نقصان في سرعة السيارة خلال مدة زمنية معينة، حتى تصل الفكرة بشكل كامل، يمكننا توضيح المفهوم من خلال الجدول الآتي:
| الجدول (1) | السرعة الثابتة، والسرعةُ المُتغيّرةُ | ||||
| الزمن (s): | t1=0 | t2=1 | t3=2 | t4=3 | t5=4 |
| سرعة السيارة الأولى (m/s): | v1=4.0 | v2=4.0 | v3=4.0 | v4=4.0 | v5=4.0 |
| سرعة السيارة الثانية (m/s): | v1=0 | v2=2.0 | v3=4.0 | v4=6.0 | v5=4.0 |
نلاحظ أن سرعة السيارة الأولى لا تتغير خلال الزمن تبقى ثابتة المقدار عن نفس السرعة وكذلك اتجاهها مما يعنى أنها لا تتسارع، أما سرعة السيارة الثانية فهي متغيرة المقدار بحيث تزداد كل ثانية من الزمن مما يعني أنها تتسارع.
التسارع ثابت ← السرعة تتغير بمقدار محدد..
التسارع المتوسط: (a)
كمية متجهة تعطى بناتج قسمة التغير في السرعة اللحظية (Δ۷) على المدة الزمنية اللازمة لإحداث التغير في السرعة (Δt).
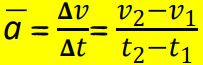
يقاس التسارع بوحدة (m/s)، ويكون اتجاه التسارع دائما في نفس اتجاه التغير في السرعة اللحظية (ΔV).
التسارع اللحظي: التسارع عند لحظة زمنية معينة.
سؤال: انطلق سامر بزلاجته بسرعة ابتدائية (2.4m/s) باتجاه الشرق، وبعد مدة زمنية مقدارها (3s) توقفت الزلاجة عن الحركة. جد مقدار التسارع المتوسط للزلاجة وحدد اتجاهه؟
الحل:
![]()
إشارة التسارع المتوسط سالبة وبالتالي يتجه نحو الغرب (x-) عكس اتجاه السرعة وفي مثل هذه الحالة تكون الحركة بتباطؤ.
حالات تسارع الأجسام
- الحالة الأولى ← تكون الاجسام متسارعة عندما تتشابه إشارة السرعة مع التسارع (يتسارع الجسم مع اتجاه السرعة) وفي هذه الحالة حركة الجسم في تزايد تكون الإشارتين موجبتين أو سالبتين.
- الحالة الثانية ← تكون الاجسام متباطئة عندما تختلف إشارة السرعة عن التسارع (يتسارع الجسم عكس اتجاه السرعة) وفي هذه الحالة حركة الجسم في تباطؤ الإشارتين أحدهما موجبة والأخرى سالبة.
تمثيل الحركة بيانيا
منحنى الموقع (الزمن):
- منحنى بياني يصف التغير في موقع الجسم بالنسبة للزمن بحيث يحدد محور ( x+) لتدريج الزمن ومحور (y+) لتدريج الموقع.
- نقطة الإسناد من المفترض أن تكون عند (0,0).
كمثال شرح لفكرة المنحنى لاحظ من خلال الشكل أن الجسم يقع على بعد (15m) من نقطة الإسناد عند اللحظة t=1s) وأنه قد غيّر موقعه ليصبح على بعد (30m) عند اللحظة (t=4s).
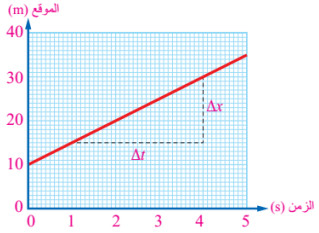
Δx = x2 – x1 = 30 – 15 = 15 m
= 1 – 4 = =Δt = t2 – t1
3s
يمكن حساب الميل من خلال القانون:
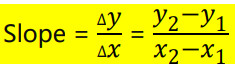
حساب الميل للمنحنى السابق:
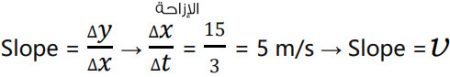
لاحظ أن الميل هنا يمثل مقسوم الموقع (المسافة) على الزمن وهي تمثل السرعة المتجهة المتوسطة.
- منحنى (الموقع – الزمن) يكون خطا مستقيما عند الحركة بسرعة ثابتة حيث التسارع يساوي صغرًا ولا يكون مستقيما عند الحركة بسرعة متغيرة حيث التسارع لا يساوي صغرًا.
منحنى السرعة (الزمن):
منحنى بياني يصف التغير في سرعة الجسم بالنسبة للزمن بحيث يحدد محور ( x+) لتدريج الزمن ومحور (y+) لتدريج السرعة.
- نقطة الإسناد من المفترض أن تكون عند (0, 0).
- يمكننا معرفة سرعة الجسم عند أي لحظة زمنية معينة من خلال الشكل وحساب تسارع الجسم من خلال تحليل الرسم البياني وحساب الميل.
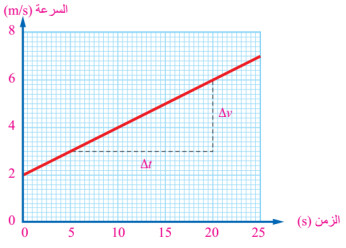
- ميل الخط المستقيم في هذا المنحى يمثل التسارع.
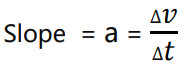
- الميل يكون موجبا عند تسارع الجسم (تتزايد سرعته) ويكون سالبا عند تباطؤ الجسم (تتناقص سرعته).
- نستفيد من منحنى السرعة – الزمن في معرفة إزاحة الجسم وذلك من خلال إيجاد المساحة تحت المنحنى.
الإزاحة = المساحة المحصورة تحت منحنى السرعة – الزمن.
سؤال: جد المساحة المحصورة بين المنحنى ومحور ( x ) بين اللحظتين (s25-0s) في المثال السابق. أو ما هي إزاحة العربة خلال المدة الزمنية (s25-0s)?
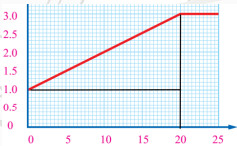
الحل:
الإزاحة = المساحة المحصورة تحت منحنى السرعة – الزمن.
الإزاحة = مساحة المثلث + مساحة المستطيل الأول + مساحة المستطيل الثاني =
(0.5×القاعدة × الارتفاع) + (الطول العرض ) + (الطول ×العرض)=
m55 = 15 + 20 + 20 = 5 × 3 + 1 × 20 + 2 × 20 × 0.5
معادلات الحركة بتسارع ثابت
معادلات رياضية تساعد على وصف الحركة المنتظمة للأجسام في خط مستقيم.
المعادلة الأولى:
V2 = V1 + at
![]()
المعادلة الثانية:
Δx=v1t+1/2at²
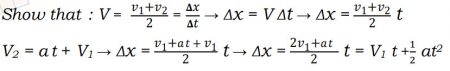
المعادلة الثالثة:
v2²=v1²+2aΔx
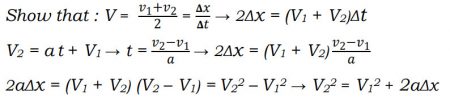
ملاحظة: الاشتقاق الرياضي لمعادلات الحركة للمطالعة الذاتية.
ملاحظات مهمة:
- استخدام أي من هذه المعادلات لحل المسائل يعتمد على ما هو معطى في السؤال: وما هو مطلوب.
- عند نقطة البداية تكون (0=t1) و (0=x1)
Δx = x2 – x1 = x2 – 0 = x2
Δt = t2 – t1 = t2 – 0 = t2
- إذا أنطلق الجسم من السكون فإن (0= V1).
- إذا توقف الجسم المتحرك عن الحركة بعد فترة فإن (0 = V2).
- إذا تحرك الجسم بسرعة ثابتة فأن a=0 ← (V1 = V2
السقوط الحر
سؤال: وضح ما هو المقصود بالسقوط الحر؟
ج: حركة الأجسام إلى الأعلى أو إلى الأسفل تحت تأثير قوة الجاذبية الأرضية فقط وذلك بإهمال القوى الأخرى مثل مقاومة الهواء.
هنا يبدأ تعاملنا بالحركة في بعد واحد على محور (y) حيث يتحرك الجسم إما نحو الأعلى ( قذف) (y+) أو نحو الأسفل (سقوط أو قذف) (y-).
حركة عمودية رأسية
ملاحظات مهمة:
- الجسم الموجود في مجال الجاذبية الأرضية يتأثر بقوة جذب الأرض له.
- السقوط الحر من أهم التطبيقات على الحركة في بعد واحد بتسارع ثابت.
- يرمز لهذا التسارع الثابت بـ (g) وهو يمثل تسارع السقوط الحر.
- يختلف تسارع الأجسام عند سقوطها بسبب تأثير مقاومة الهواء لها وهذا التأثير يختلف باختلاف حجم وشكل وسرعة الجسم الساقط.
- تسارع الجاذبية ثابت مقداره وهو يساوي g= 9.8 m/s) نحو سطح الأرض.
- في حالة السقوط الحر أو قذف جسم نضع في معادلات الحركة السابقة ( g- ) بدلا من (a) و (y) للتعبير عن الإزاحة الرأسية بدلًا من الإزاحة الأفقية (x) و (h) للتعبير عن الارتفاع.
- الإزاحة والسرعة تكون موجبة إذا كانت الحركة للأعلى وسالبة إذا كانت الحركة للأسفل.
- تسارع الجاذبية (g) يكون دائماً سالب لأن اتجاه تسارع الجاذبية دائما نحو الأسفل بغض النظر عن مكان نقطة الإسناد أو اتجاه الحركة.
- ممكن تكون الإزاحة الرأسية تساوي الارتفاع وممكن تختلف، يعتمد ذلك على المطلوب بالسؤال.
- الارتفاع دائما موجب على عكس الإزاحة الرأسية ممكن تكون موجبة وممكن سالبة.
- عند عودة الجسم المقذوف من مستوى معين إلى نفس المستوى تكون إزاحته (0=y). لذلك حسب المعادلة (V2²= V1²+ay2) ← فإن (V2) = (V1 ) إلا Hنهما متعاكسان في الاتجاه.
- ناتج الجذر التربيعي يكون (+) و (-) القيمة ونختار قيمة ونهمل قيمة حسب اتجاه الحركة.
- سرعة الصعود من نقطة ما تساوي في المقدار سرعة الهبوط إلى النقطة نفسها.
سؤال: أسقطت كرة من وضع السكون كما في الشكل فوصلت الأرض بعد ( 0.6s )K جد السرعة النهائية للكرة قبل ملامستها سطح الأرض مباشرة؟
الحل:
V1 = 0 m/s ,g = 9.8m/s² ,t = 0.6 s
V2 = V + at → V2 = V1 – gt
V2 = 0 – 9.8 × 0.6 → V2 = -5.88 m/s
الإشارة السالبة هنا تعني أن اتجاه السرعة نحو الأرض بعكس الاتجاه الموجب.
سؤال: في السؤال السابق جد الارتفاع الذي سقطت منه الكرة؟
الحل:
V1 = 0 m/s , g = 9.8m/s², t = 0.6 s, V2 = -5.88 m/s
y=v1t+1/2at²=v1t-1/2gt²=0×0.6-0.5×9.8× (0.6)²
y =-1.764 m→ h = 1.764 m
تدريب؟ قام عوض برمي حجر رأسيا نحو الأعلى بسرعة ابتدائية (10m/s)،جد:
- سرعة الحجر عند عودته لسطح الأرض.
- الزمن الذي استغرقه الحجر ليعود إلى سطح الأرض.
تدريب؟ قام نيشان بقذف حجر رأسيا نحو الأسفل بسرعة ابتدائية (10m/s)،جد:
- a) سرعة الحجر عند وصوله سطح الأرض.
- b) الزمن الذي استغرقه الحجر ليصل إلى سطح الأرض.
حل أسئلة مراجعة الدرس الأول من الوحدة الثانية
سؤال: وضح المقصود بالحركة المنتظمة في بعد واحد وعلاقة ذلك بالسرعة والتسارع؟
ج: حركة الجسم بسرعة قياسية ثابتة المقدار إما بشكل أفقي أو عمودي. عندما تكون الحركة منتظمة تكون السرعة ثابتة والتسارع يساوي صغرًا.
سؤال: تحرك قطار حركة أفقية في خط مستقيم بسرعة ثابتة مقدارها (12m/s). جد الإزاحة التي يقطعها القطار إذا تحرك مدة (80s).
الحل:
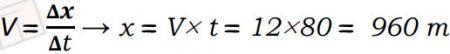
سؤال: تسحب فتاة صندوقًا على سطح أفقي في اتجاه ثابت، وقد بدأ الحركة من وضع السكون، وأصبحت سرعته 1.2m/s بعد مرور (3s). جد التسارع الذي أكتسبه الصندوق؟
الحل:
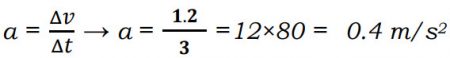
سؤال: يمثل الشكل الآتي منحى الموقع – الزمن لحصان يجر عربة في طريق، معتمدًا على الشكل جد ما يأتي:
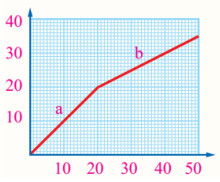
- الإزاحة التي قطعتها العربة في المرحلة (a) من الحركة.
الحل:
Δx = x2 – x1 = 20 – 0 = 20 m
- السرعة المتوسطة للعربة في المرحلة (b) من الحركة.
الحل:

سؤال: يجري عداء في طريق مستقيم، رصدت حركته ومثلت سرعته بيانيًا كما في الشكل. معتمدًا على الشكل جد ما يأتي:
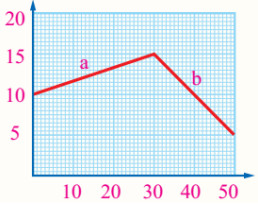
- السرعة اللحظية للعدّاء عن نهاية المرحلة (a) من الحركة.
ج: V = 15 m/s
- تسارع (تباطؤ) العدّاء في المرحلة (b) من الحركة.
الحل:
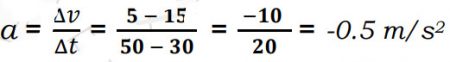
- الإزاحة التي قطعها العدّاء في مرحلتي الحركة معًا.
الحل:
الإزاحة = المساحة المحصورة تحت منحنى السرعة – الزمن.
إزاحة المرحلة (a) =
مساحة المثلث + مساحة المستطيل = (0.5×القاعدة × الارتفاع) + (الطول ×العرض).
الإزاحة = 0.5 × 30 × 5 + 10 × 20 = 75 + 200 = m 275
إزاحة المرحلة (b) =
مساحة المثلث + مساحة المستطيل = (0.5×القاعدة × الارتفاع) + (الطول ×العرض)
الإزاحة = 0.5 × 20 × 10 + 5 × 20 = 100 + 100 = 200 m
الإزاحة التي قطعها العداء = إزاحة المرحلة (a) + إزاحة المرحلة (b) = 475 m
⇐ درس مُقترح للمراجعة: إجابات & حل أسئلة الوحدة 1 «المتجهات» فيزياء 10 «أردني» الفصل الأول